Вопрос, связанный с методикой изучения математики

[BENEDIKT]

Прошу прощения у уважаемых участников форума, если мой вопрос покажется странным.
Допустим, имеет место следующее. При прочтении доказательства какой-либо теоремы понятны исходные утверждения, на которых это доказательство строится (это материал уже изученных предыдущих разделов). Само же по себе доказательство понятно лишь как цепь алгебраических преобразований, в результате которых исходное (понятное) выражение превращается в то, что, собственно, и доказывалось. Однако "математический смысл" доказанного, связанный с тем или иным конкретным разделом, сам по себе неясен. Т. е. понятно, как придти к данному выражению, осуществив такие же преобразования, какие предлагают авторы учебника, но не более того.
Точно так же и промежуточные утверждения, формулируемые при доказательстве теоремы, понятны лишь как результаты алгебраических преобразований, но смысл их с точки зрения конкретного изучаемого раздела (будь то геометрия, тригонометрия линейная алгебра, математический анализ и пр.) не понятен.
Допустимо ли это? И в каких масштабах? Неприятно, когда смысл чего-то остаётся неясным, даже если понятны все преобразования. И можно ли принимать что-то "на веру"? Особенно, если желаемый уровень понимания того или иного раздела "царицы наук" не ограничивается примитивной способностью механически решать простенькие типовые задачи?
P.S. Вопрос касается в первую очередь самой математики и отчасти - тех наук, в которых она применяется.

[Munin]

Ответ, насколько я представляю: бывает по-разному.

В самой математике есть два противоположных течения. С одной стороны, есть течение (и математики - приверженцы такого подхода), чтобы сделать математическое доказательство на основе ясной идеи, кратким и очевидным. При этом можно менять сам доказываемый факт, выражать его в таких понятиях и в таком виде, который лучше всего подходит для такого доказательства. При этом получаются очень глубокие обобщения и аналогии. С другой стороны, есть течение, в котором именно наличие доказательства - самоцель, а его длина, техническая сложность, использование глубоких идей - это уже всё вторично. Этот путь позволяет, в конце концов, разрешить те вопросы, которые долго мучали математиков.

С другой стороны, есть преподавание математики. Большинство фактов, изложенных в начальных учебниках, скажем, для младших курсов, - относятся к первому типу, к фактам, для которых известны ясные и глубокие доказательства (иногда самоочевидные, как только будет ясен смысл утверждения). Но вот не во всех учебных курсах именно такие доказательства даны. Иногда автор курса придерживается какой-то традиции, иногда он просто сам не в курсе, или не желает привести более прозрачное и понятное доказательство. Получается, что математические курсы бывают лучше или хуже с этой точки зрения. Но не всё так однозначно. Есть корреляция: чем более ясного изложения придерживается курс, тем более глубокого знания он требует от учащегося. Прозрачные вещи прозрачны для того, кто достаточно тренирован, чтобы их воспринимать.

Например, довольно многие факты наиболее просто формулируются и доказываются, если их рассматривать как относящиеся к пространствам произвольной (конечной) размерности $n.$ Но читатель может быть не готов к тому, чтобы вообще воображать себе такие пространства и соотношения в них, и ему проще было бы разобраться с менее глубокими и более надуманными доказательствами, но относящимися к простым случаям $n=1,2$ или $3.$

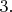
И с третьей стороны, отдельно в новом обличье эта проблема возникает в случае, когда математический факт используется в других науках. Здесь часто есть нехватка не математического, а прикладного смысла. И в отличие от самой математики, известные доказательства даже начальных фактов часто с этим прикладным смыслом не связаны. Но здесь есть и другой подход: можно восстанавливать прикладной смысл доказательства самостоятельно. Пройти по всему доказательству, и разобраться, что означает каждый его шаг, если переводить его на прикладной (например, физический) язык.

[BENEDIKT]

Большое спасибо за ответ.

[Munin]

Может, стоило задать этот вопрос в разделе "Вопросы преподавания"? Или в корне "Математики"? Я думал, ответят больше людей. Моего ответа явно недостаточно, я знаю эти вопросы довольно по касательной. Ориентируюсь на то, что мне о вас известно.

С другой стороны, если вы приведёте конкретный пример, какое именно доказательство (или какие именно доказательство) вам неясно по смыслу, можно было бы разобраться с таким примером. Но это совсем другой поворот темы, а не общий вопрос, который вы задали. Может быть, стоит задать такой конкретный вопрос в другой теме.

[Toucan]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Вопросы преподавания»
Причина переноса: просьба ТС

[Toucan]

Обсуждение интеграла Лебега отделено сюда: «Не могу постичь теорию меры и интеграл Лебега»

[BENEDIKT]

В продолжение темы. Надеюсь, уважаемым участникам форума не покажется странным такой вопрос. Допустимо ли, хотя бы на первоначальном этапе, использование таблицы производных без понимания всех её значений?
Скажем, легко понять, почему производная константы равна 0, производная аргумента равна единице. Приращения у постоянной функции нет, а приращение аргумента равно приращению аргумента. Наглядно видно, что производная линейной функции $y=kx+b$ равна $k$: касательная к ней есть параллельная ей прямая, т. е. прямая с тем же угловым коэффициентом, которому и равна производная. А скорость изменения функции "явно" равна $k$, т. к. это коэффициент при $x$.
Но более сложные примеры не позволяют так чётко "увидеть" производную. Например, "не видно", почему производная функции $y=x^n$ равна $nx^{n-1}$, производная функции $y=\sin x$ равна $\cos x$ и т. д.
Хотелось бы понимать смысл математических операций достаточно глубоко, а не просто уметь решать механически. Нормально ли бездумно использовать значения таблицы производных, не понимая, почему скорость изменения той или иной функции описывается именно так, а не иначе? При том, что доказательства формул производных основных функций даны автором в учебнике и понятны.

[arseniiv]

BENEDIKT в сообщении #853185 писал(а):

Например, "не видно", почему производная функции $y=x^n$ равна $nx^{n-1}$, производная функции $y=\sin x$ равна $\cos x$ и т. д.

Имеете в виду, что как предел её нашли, но это не впечатлило? Может, стоит тогда ещё нарисовать графики и проследить, что «на глаз» производная действительно напоминает производную?

Таблицу смело можно использовать, даже если вы вывели её строки механически или заверили себя, что способны вывести некоторые не выведенные на момент использования, считаю (импликация здесь только справа налево и не обратно).

[provincialka]

BENEDIKT, а у какого количества функций вы бы хотели понять смысл производной? У простейших элементарных (школьных) функций? У элементарных (записанных формулой)? Еще у каких-то? Мне кажется, если вы усвоили геометрический и "динамический" смысл производной, этого достаточно.

[ewert]

BENEDIKT в сообщении #853185 писал(а):

Допустимо ли, хотя бы на первоначальном этапе, использование таблицы производных без понимания всех её значений?

Допустимо. А в каком-то смысле даже и необходимо.

BENEDIKT в сообщении #853185 писал(а):

Но более сложные примеры не позволяют так чётко "увидеть" производную.

Естественно. Но тут уж так: ежели вам нужно всего лишь ехать -- плюньте на шашечки (в конце-то концов, не думаете же Вы, что все эти яйцеголовые Вас обманывают). И только если захочется действительно разобраться, откуда какие ноги растут -- только тогда и задумывайтесь.

Вообще практически невозможно разобраться ни в какой теории так с нахрапу и сразу до конца. "До самой сути: В работе, в поисках пути, В сердечной смуте..." Это возможно лишь методом последовательных приближений.

[Munin]

Таблица производных маленькая, и вывести её всю целиком (несколько пунктов списав из учебника) - не слишком большое упражнение. А после этого вы получаете моральное право её всю целиком и использовать.

[BENEDIKT]

provincialka в сообщении #853192 писал(а):

BENEDIKT, а у какого количества функций вы бы хотели понять смысл производной? У простейших элементарных (школьных) функций?

Да, пока что хотя бы у них.

arseniiv, provincialka, ewert, Munin
Большое спасибо всем за разъяснения.

[Munin]

BENEDIKT в сообщении #853185 писал(а):

Хотелось бы понимать смысл математических операций достаточно глубоко, а не просто уметь решать механически.

Про "смысл" я рассказывал, кажется, вам же, достаточно много.

Нет никакого особенного "смысла" математических операций, кроме того, который вытекает из их определения, свойств, использования и применения.

Так что, сначала вы решаете "механически", пусть вам это и не нравится. И постепенно, через 100 задач, через 1000 задач, начинаете "понимать что-то такое, глубокое".