Замыкание множества

[Alex_J]

Задачка. Показать, что в евклидовой топологии на $\mathbb{R}$ множество $S_1=\{0,1,\frac 1 2, \frac 1 3,...,\frac 1 n, ...\}$, $n\in\mathbb{N}$ замкнуто, и выяснить, является ли замкнутым множество $S_2=\{1,\frac 1 2, \frac 1 3,...,\frac 1 n, ...\}$.

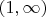
Здесь всё вроде ясно, кроме предельного случая. Если считать $S_1$ замкнутым, то дополнение до $\mathbb{R}$, а именно, $\P_1=\mathbb{R}\setminus S_1$ открыто. Оно представляет собой объединение открытых множеств $(-\infty,0)$, $(1,\infty)$, а также $\bigcup\limits_{n=1}^{\infty}(\frac{1}{n+1},\frac 1 n)$.

Как быть с первым интервалом справа от нуля? Пусть $x\in P$,$x>0$, тогда должны найтись $\exist a, b \in \mathbb{R}$ такие, что $x\in(a,b)\subseteq S_1$, в силу определения евклидовой топологии. Пусть $a=0$. Тогда, с одной стороны, для любого $b$ есть $n$ такой, что $0<\frac 1 n<b$, с другой, в силу произвольности выбора $b$, мы можем потребовать, что наоборот $0<b<\frac 1 n$.

Каков выход?

[Oleg Zubelevich]

используйте язык последовательностей

[kp9r4d]

Oleg Zubelevich в сообщении #846384 писал(а):

Как быть с первым интервалом справа от нуля?

Интервалы не обязательно должны быть вполне упорядочены, в частности «первого» может не найтись, как сейчас вот.

[Alex_J]

Тогда лучше остаться в пределах рассуждения такого, что в интервале $(0,1)$, в котором есть бесконечно много точек множества $S_1$, есть и бесконечно много интервалов вида $(\frac{1}{n+1},\frac 1 n)$, и любая точка $x\in P$, как уже показано, имеет свою окрестность внутри одного из интервалов, и этого вполне достаточно, и тогда $S_1$ - замкнуто.

А $S_2$ отличается от $S_1$ отсутствием точки 0 и тоже замкнуто.

[Otta]

Да что ж так тягостно-то все у Вас. Вы же в самом первом посте еще написали - дополнение к Вашему множеству это $\bigcup\limits_{n=1}^{\infty}(\frac{1}{n+1},\frac 1 n) \cup (-\infty,0)\cup (1,\infty)$. Только зачем все эти лишние слова и предположения? Каждый интервал - открыт, объединение любого числа открытых - открыто, что-то еще надо?

Но я бы в жизь так не делала, понятно, что множество содержит все свои предельные точки. Все. Это Вам и предлагали с самого начала.