Спасибо,
Otta. Можно если я скатаю остальное с учебника как есть чтоб задавать вопросы по ходу? Переводить на русский все это просто гимор.
Let us now assume that our theorem is true for a system of
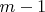
equations in more than
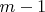
unknowns. We shall prove that it is true for

equations in

unknowns when

. We consider the system [above].
If all coefficients
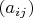
are equal to

, we can give any non-zero value to our variables to get a solution. If some coefficient is not equal to

, then after renumbering the equations and the variables, we may assume
that it is
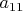
. We shall subtract a multiple of the first equation from the others to eliminate

. Namely, we consider the system of equations
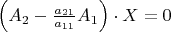

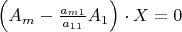
,
Which can be written also in the form
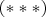
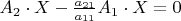

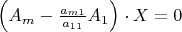
In this system, the coefficient of

is equal to

. Hence we may view
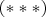
as a system of
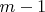
equations in

unknowns, and we have

.
According to our assumption, we can find a non-trivial solution

for this system. We can then solve for

in the first equation,
namely
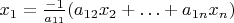
.
In that way, we find a solution of
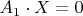
. But according to
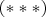
, we
have
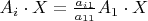
for
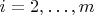
. Hence
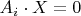
for
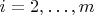
, and therefore we have found a non-trivial solution to our original system

. [






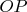
] The argument we have just given allows us to proceed stepwise from
one equation to two equations, then from two to three, and so forth.
This concludes the proof.
-----------------------------------------------------------------------------
Пойду-ка я пока поизучаю это док-во. Вернусь с вопросами.