Уважаемый Talinkin,
в рассматриваемом случае всегда

.
Если

-простое число, то

должно делиться на
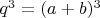
.
Поскольку

меньше

, то частное от деления будет рациональной дробью.
Аналогичный результат будет и в том случае, если двучлен
 ,
, т. е. произведению простых чисел каждого в первой степени.
Доказательство надо искать для случая, если

.
При этом надо учесть, что значения числа

, если оно целое, лежат в пределах:

(1)
Поскольку

нечетное число, то его возможный наименьший делитель равен

.
Если, например, двучлен

, то его в соответствии с соотношением (1) нельзя сокращать на

.