незваный гость писал(а):
:evil:
Tried. Solved.
1) Lets take an arbitrary
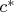
and construct a triangle from it and two given angles. Obviously it is similar to the one we need. So we can measure its median
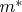
and construct

from proportion
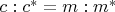
.
BTW, the approach works with any “two angles, one linear element” problem.
2) I do not see anything but exercise in typing here. The area can be expressed thru
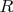
and angular functions, the square of median — too.
ins- писал(а):
I know the triangle is defined by any 3 elements from my school teacher in math.
Oh, those authorities.

Try a triangle

,
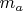
,
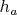
. Or a triangle

,
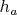
,
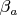
.
You are right my problem is not difficult but it is not 'obvious' that the triangle is defined by these elements. a ) is from a book. b ) is composed by me I don't took in mind this I used that
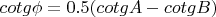
Where
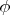
is the angle between
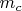
and AB. If you want something difficult -

solve my open problem 1 - 'beautiful and difficult'.

First triangle is defined by its 3 elements algorithm for construction:
1. Construct a.
2. Draw a line g parallel to a and distance between a and g is
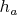
.
3. Draw a circle k with center middle of A and with radius
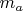
.
4. A is intersection point of k and l.
In this case we may construct 0, 1, 2, 4 triangles but no matter how they are if it exists it is the same triangle.
I don't know what you want to say with
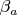
for your second example.