Случайное блуждание, дисперсия

[Slumber]

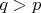
У меня есть случайное блуждание (процесс рождения - гибели), стартующее из нуля. Нужно найти дисперсию времени возврата в $0$. Вероятность гибели $q>p$ вероятности рождения, $p+q=1$.

Есть время возврата из 1: У Феллера (Том 1, Гл 14, §4 в русском - стр 345, (4.12), (4.8)) есть производящая функция для процесса, стартующего из $z=1$:
$U_1(s) = \mathlarger{\frac{1 - \sqrt{1-4pqs^2}}{2ps}}$

Обозначим время возврата из 1 как $Y_1$. Тогда, первый и второй моменты будут соответственно
$E[Y_1] = U'_1(1), \ E[Y_1^2] =U''_1(1) + U'_1(1)$.

(Оффтоп)

http://en.wikipedia.org/wiki/Probability-generating_function

Матожидание я успешно нашел (сходится с расчетами в лоб программой):

(Оффтоп)

по формуле полного матожидания:
$E[X_1] = (E[Y_1]+1)\cdot p + 1\cdot q$
- то есть, если на первом шаге частица или сдвинулась на $+1$, тогда время ее возврата в $0$ составит $Y_1+1$, или осталась в нуле, тогда время восстановления для нее будет равно $1$.
Формально будет выглядеть
$\mathrm{E} [ X_1 ] = \mathrm{E}[ X_1 \ | \zeta_1 = 1]\mathrm{P}(\zeta_1 = 1) + \mathrm{E}[ X_1 \ | \zeta_1 = 0]\mathrm{P}(\zeta_1 = 0)$
Для вольфрама:

p := 0.2
u[p_, s_] := (1 - Sqrt[1 - 4 p (1 - p) s^2])/(2*p*s)
g[s_] := u[p, s]
h[p_] := (g'[1] + 1)*p + (1 - p)
h[p]
Out[74]= 1.33333

Проблема с дисперсией. Я точно так же беру формулу полной дисперсии ($E[E[X|Y]] = E[X]$):

$D[X] = E[D[X|Y]] +D[E[X|Y]] = E[D[X|Y]] + \big( E[(E[X|Y])^2] - (E[X])^2 \big)$

Первое слагаемое - вот как ее правильно просуммировать с $1$ ?
$E[D[X|\zeta_1]] = ((D_1 + 1)\cdot P(\zeta_1=1) + 1\cdot P(\zeta_1=0))$
$D_1=E[Y_1^2] =U''_1(1) + U'_1(1)$

Второе слагаемое, обозначим матожидание $U_1'(1)=M_1$, а $E[X]$ посчитали выше :
$\big( (M_1+1)^2 p + (1)^2 q \big) - ( E[X] )^2$

Вольфрам:

(Оффтоп)

p := 0.2
u[p_, s_] := (1 - Sqrt[1 - 4 p (1 - p) s^2])/(2*p*s)
g[s_] := u[p, s]
h[p_] := (g'[1] + 1)*p + (1 - p)
h[p]
Out[74]= 1.33333
d1 := g''[1] + g'[1] - (g'[1])^2
f[a_, p_] := (((a + 1)^2)*p  + ((1 )^2)*(1 - p)) - (h[p])^2
hh[p_] := ((g''[1] + g'[1] - (g'[1])^2 + 1)*p + 1*(1 - p))
hh[p] + f[g'[1], p]
Out[76]= 2.03704

Но этот ответ с моим расчетом не сходится (~1.0...):
http://d.cc.ua/misc/dispersion.cpp

Причем, даже, если убрать единицу, все равно выходит много.

[--mS--]

Воспользуйтесь тем, что $X_1=Y_1\cdot \zeta_1+1$, где $Y_1$ и $\zeta_1$ независимы. Дисперсия $X_1$ элементарно считается:

$$\mathsf DX_1 = \mathsf D(Y_1\zeta_1)=p\mathsf EY_1^2 - p^2(\mathsf EY_1)^2. $$

(Оффтоп)

Только это не процесс рождения и гибели никак.

[Slumber]

Спасибо большое, кажется работает.

(Оффтоп)

Согласен, пускай будет Discrete Time Birth-Death Process. Кто-то употребляет )).
http://journals.cambridge.org/article_S0334270000007621
http://www.jstor.org/stable/3215173

Но работают вещи, посчитанные для непрерывного времени.

Например, я брал еще для $E[Y_1]$ (из 1) известный результат $(\mu = q, \lambda = p)$:
стр 149 самой книги
http://www.scribd.com/doc/158016727/A-First-Course-in-Stochastic-Processes-2nd-Edition-Karlin-Taylor
$\omega_1 =\mathlarger{\sum_{i=1}^{\infty} \frac{\lambda_1 \lambda_2 ... \lambda_{n-1}}{\mu_1 \mu_2 ... \mu_n}} = \mathlarger{\sum_{i=1}^{\infty} \frac{\lambda^{n-1}}{\mu^n}} = \mathlarger{\frac{1}{\mu} \sum_{i=0}^{\infty}\frac{\lambda^{n-1}}{\mu^{n-1}}} =\mathlarger{\frac{1}{\mu - \lambda}} $
$\mathrm{E}[ X_1 \ | \zeta_1 = 1] = \omega_1 + 1 = \mathlarger{\frac{1}{\mu-\lambda} +1} $
$\mathrm{E} [ X_1 ] = \mathlarger{\big( \frac{1}{\mu - \lambda} + 1 \big) \cdot \lambda + 1 \cdot \mu}$
И это численно сходится с полученным через производящую функцию. В другой книжке есть и $E[Y_1^2]$, но выражение очень громоздкое.