Есть ур-ние:
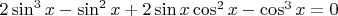
1) Сначала попробовал так: взял один "кибический синус" и объединил с "кубическим" косинусом и раскрыл разность кубов:
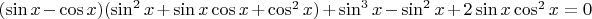
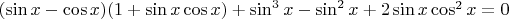
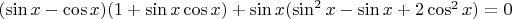
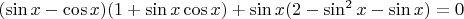
В правой скобке можно, конечно, разложить квадратный трехчлен, но мне это особо не помогло. Дальше не знаю куда двигаться
2) пробовал второй вариант: вынести за скобку
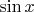
и
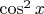
.
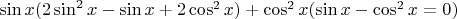
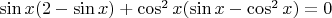
И тут дальше не знаю что делать...
3) поделить на
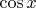
не можем, т.к., если вдруг
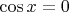
, то останется уравнение, имеющее конкретную серию корней
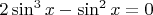
деление на
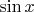
, на мой взгляд, ни к чему хорошему не приводит...
Так что не знаю как дальше
Надеюсь, простых арифметических ошибок в вычислениях нет.