Пусть

— действительное число. Для каждого целого

обозначим через

расстояние от

до ближайшего рационального числа вида

, где

— целое. Найдите наибольшую возможную сумму ряда

.
Мне кажется это будет сумма ряда

. Мысль такая: у нас есть нитка длиной

. И каждый раз мы измеряем её длину линейкой с ценой деления
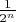
и ближайшее рациональное всегда ближе или дальше на одно деление линейки.