Значит, надо разделить окружность на

частей.
На

можно будет разделить после всего остального.
Мы умеем строить углы, равные

части окружности.

получаем как
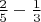
, т.е. откладываем от некоторой точки на окружности:

раза угол в

окружности в одну сторону (вперед) и

раз угол в

окружности в другую сторону (назад).
Аналогично продолжаем:

И так далее.