Простые числа. Верно ли утверждение?

[netang]

Пусть $\{x_{1}, x_{2}, …, x_{n}, x_{n+1}, …\}$ – последовательность простых чисел. Тогда для любого $x_{n}$ справедливо неравенство $ x_{n+1} < 2x_{n}+1$.

[mihailm]

Постулат Бертрана покрутите немного

(Оффтоп)

Хотя никакой он конечно не постулат

[netang]

mihailm в сообщении #822364 писал(а):

Постулат Бертрана покрутите немного

(Оффтоп)

Хотя никакой он конечно не постулат

Цитата:

Для любого натурального $n ≥ 2$ найдётся простое число $p$ в интервале $n < p < 2n$.

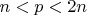
Т.е. если мы возьмем любое $ x_{n} ≥ 2$, то $x_{n+1}$ обязательно будет лежать между $ x_{n}$ и $ 2x_{n}$ т.е. $ x_{n} < x_{n+1} < 2x_{n} $ => $ x_{n} < x_{n+1} < 2x_{n}+1 $? Что в принципе мне и нужно было :)