Вот такое нау-хау.
Функция регрессии:

.
Находим

после логарифмирования.
1. Формируем три параметра

, то есть 10%-ные отклонения вверх и вниз. Для каждого параметра делаем замену переменных

Имеем три функции регрессии вида

. По МНК находим

и считаем сумму квадратов невязок

. Считая эти 3 пары координатами параболы находим

, при котором парабола имеет минимум.
2. Повторяем п.1 с новым значением

и с 5%-ным отклонением. Находим

.
3. Повторяем п.1 с новым значением

и с 1%-ным отклонением. Находим

.
4. Для функции регрессии
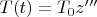
находим

по МНК.
Проверил на вашем примере, коэффициенты получаются оптимальные.