Добрый день.
Существует такая задача: Есть строка и некоторый алфавит длиной

(

в общем случае большое и можно апроксимировать). В каждый момент времени в строке появляется один символ из алфавита. Появление символов равновероятное и независимое от предшествующих. То есть строка - это бернуллиевская последовательность. Необходимо найти длину строки, при которой в ней с вероятностью
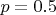
появится все символы из алфавита (хотя бы один раз). Для длины достаточна оценка снизу, главное, что бы обосновано и естественно больше чем длина алфавита.
Нигде не смог найти решение данной задачи.
Данная постановка задачи описывается полиномиальным распределением, но проблема в том что что при больших размерах алфавита не понятно как найти все выборки в которых может присутствовать ноль напротив одного из символов,
а затем просуммировать их вероятности. В принципе все такие события описываются полиномиальным распределением
для

символов. А преобразовать в соответствующую вероятность для

символов (в дальнейшем использую устояшевшиеся обозначения

- длина алфавита,

- длина строки)

, что выводится просто из сравнения формул вероятности для

и

при

опытах. Но при этом возникают дополнительные тонкие места связанные с выборкой

символов из алфавита

, что тоже легко рассчитывается. Но просто умножить их нельзя, так как в каждом из выделенных алфавитов могут быть порождены одинаковые строки, а как их учесть не понятно.
Пробовал использовать распределение Пуассона, но как работать с ним в отношении полиномиального распределения не знаю (источников пока не нашёл). А из того что получилось своими силами не понятно как привязать к данной задачи.
Смотрел обратное полиномиальное распределение. Но как его прикрутить к этой задачи не понятно, так как в ней количество опытов останавливается, когда одно из событий превысило определённый порог, а в данном случае должны превысить все события минимальный порог. Думал рассмотреть задачу как зависят вектора от максимального количества определённого события, но как к этому подойти не понятно.
В итоге я решил задачу приблизительно, но как её обосновать вопрос и рассчитать вероятность данного события при найденной длине для проверки. Для этого рассмотрел следующую схему взятия шаров из вазы с возвращением. В вазе присутствует

белых шаров. Когда мы из вазы достаём белый шар мы считаем это успешным событием, после чего его красим в чёрный цвет и кладём обратно в вазу. Теперь для каждого количества белых шаров в вазе, кроме того случая когда там уже все чёрные, мы рассчитываем количество опытов

при котором с вероятность

будет успешное событие - а именно достанем белый шар. После этого суммируем количество всех опытов и получаем примерную длину строки в которой с вероятностью

будут встречены все символы из алфавита.
