Степени дюжины

[Ktina]

Решить в натуральных числах уравнения:

а)

$$n!+m!=12^k$$

б)

$$n!-m!=12^k$$

в)

$$n!\cdot m!=12^k$$

г)

$$n!\text{.}m!=12^k$$

(символ "." обозначает конкатенацию)

[danilka666]

а)n=4 m=5 k=2
в)n=2 m=3 k=1

[DjD USB]

Первые две решаются одинаково.
1) Пусть для определенности $n \ge m$ Тогда При m>4 нет решений, т.к левая часть в этом случае будет оканчиваться на 0. И если $1<m<4$ то левая часть при $n \ge 4$ делится только на 2, но она должна делится хотя бы на 4. Если m=1, то и n=1. Очевидно это нам не подходит. Остался случай, когда m=4
m=4.

$$n!+24=12^k$$

При n>5 левая часть делится на 8 но не делится на 16, значит k=3. Но тогда нет решений.
Остались 2 случая n=5 и n=4. Получим одно решение, при n=5.
Я так думаю что-то в этом духе и в пункте б)

-- Вс янв 19, 2014 21:49:41 --

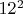
В третей совсем просто тогда Оба они меньше 5-ти. Тогда произведение меньше чем $12^3$ Причем если Убрать случай, когда m=n=4, в котором получаем, что решений нет, то тогда их произведение не меньше $12^2$. Равенство достигается при m=4, n=3. Ну и получаем, что $m!\cdot n!=12$ легко найти единственную пару m=3, n=2 и конечно же можно и наоборот взять числа. Получим 4 решения (3;4),(4;3),(2;3),(3;2)

-- Вс янв 19, 2014 22:04:56 --

В пункте г) 1<m<5 очевидно. Если m!=2 или 6, то тогда предпоследняя цифра числа n!_{\cdot}m! должна быть нечетной, что бы оно делилось на 4. Тогда n=1. Получим 1 решение m=2, n=1, k=1
Остался случай, когда m=4. Тогда если n>9 получаем что число делится на 8 но не делится на 16. Значит k=3 очевидно этот случай нам не подходит. Тогда n<10 перебираем... И получаем, что в этом случае решений нет.

[Ktina]

danilka666 в сообщении #816700 писал(а):

а)n=4 m=5 k=2
...

А второе решение пункта a) Вы потеряли

[DjD USB]

Ktina в сообщении #816807 писал(а):

danilka666 в сообщении #816700 писал(а):

а)n=4 m=5 k=2
...

А второе решение пункта a) Вы потеряли

Ах да. В самом начале при $1<m<4$ получили, что $n<4$. Получим еще 1 решение (3;3;1)

[Ktina]

Пункт а):

При $k\geqslant 3$ одному из двух факториалов придётся делиться на 9, так как все факториалы, начиная с $6!=720$, делятся на 9.
Но тогда и второму факториалу тоже придётся делиться на 9, ведь все степени 12, начиная со второй, кратны 9.
Только вот если факториал делится на 9, то он неизбежно делится и на 5, откуда немедленно следует отсутствие решений для $k\geqslant 3$.
Остальное -- перебором:
$3!+3!=12^1$
$5!+4!=12^2$

[Ktina]

Пункт б):

Ответ: Решений нет.

Если $k=1$, то перебором находим, что нет двух факториалов с разностью 12.
При остальных $k$ если $n!$ кратно 9, то и $m!$ должно быть кратно 9, но тогда они оба кратны 5, что невозможно.
Если же $n<6$, то $12^k$ меньше 120, что возвращает нас к случаю $k=1$.