Сложная задача с параметром

[Solutions1]

Здравствуйте!
Помогите, пожалуйста, решить задачу:
Найти все положительные значения a, для которых система не имеет решений.
$16x^2+(4-5a)(x^3+x)-5/4a(x^2+1)^2\leqslant0$;
$4x/(x^2+1)=(1-y)/(5y)+ay/(1-y)+a/4$;
$0<y<1$.
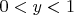
Я преобразовал первое неравенство системы к виду: $(x^2+4x+1)(5ax^2-16x+5a)\geqslant0$. Далее, я стал пытаться упростить второе уравнение, но ни чего толкового не вышло. Я еще пробовал выразить либо $x^2+1$, либо $x$ из второго уравнения и подставить в первое неравенство, для того чтобы избавиться от переменной $x$. У меня это вышло, но что делать дальше я не знаю.
Жду вашей помощи.

[provincialka]

Некоторые мысли...
1. В уравнение $y$ входит только в составе выражения $\frac{1-y}{y}=t$. Какие значения принимает эта переменная?
2. Неравенство можно разделить на $(x^2+1)^2$, тогда $x$ будем входить в него только в составе выражения $\frac{x}{x^2+1}=z$. Какие значения оно может принимать в силу этого неравенства?
3. В уравнении левая часть зависит только от $z$, а правая - только от $t$. При каком условии оно имеет решение?

[Solutions1]

Я уже делал эту замену и указывал для нее область значений ($t>0$), но ведь условия существования этого уравнения зависит от $x$ ($x>0$). Но чтобы сделать ограничения по $x$, я использовал третье неравенство, а это может и неверный шаг.

[provincialka]

Не поняла ваших слов. Посмотрите. я там добавила в ответ. Думаю, решение надо отложить на завтра, уже полтретьего ночи.

[Otta]

Если аккуратно преобразовать первое неравенство, предварительно сделав замену $u=\frac{x}{x^2+1}$, то будет видно, что $u=-1/2$ является его решением при всех значениях параметра. Значит, первый шаг - выяснить, при каких значениях параметра $a\;$ $u=-1/2$ не является решением уравнения. Попробуйте дальше сами.