Я не слежу за вашими выкладками, но независимость работы от момента инерции как-то странно мною воспринимается.
Ну чтобы не заморачивать себя вращениями, возьмите аналогию в обычном движении. Есть точка, причём
её траектория движения задана. Известно, какая сила была приложена на каждом участке траектории. Очевидно, работа будет просто

и масса в её выражение не войдёт. Точка может быть даже не свободной, например, она может быть кончиком рычага машины, который мы рукой двигаем. Какая нам разница, какая у него масса?
-- 18.01.2014 13:48:45 --а то, что ниже написано зачем нужно, при том, что известно

?
Затем, чтобы прояснить момент с независимостью ответа от
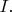
ну значит задача на эту техническую работу, можно переносить в олимпиадный раздел :D
Да ну, кто вообще

параметризует углами Эйлера? Это же неудобно. Их парамеризуют матрицами Паули. Эйлер жил в 18 веке, и его координаты устарели.
динамику, кстати, учесть невозможно
А, ну да, не прочёл этого.
кроме того, ни где не сказано, что

это неподвижная точка или центр масс
А вот это учесть динамику не помешало бы.
Ну ладно, задача решена, отрясаем мел с рук своих, и идём дальше по своим делам.