Возгорание

[randy]

В спектре излучения огненного шара радиусом $100$ м, возникающего при ядерном взрыве, max излучения приходится на $\lambda = 0,29$ мкм. Найти max расстояние (L), на котором будет загораться дерево с поглощательной способностью $0,7$. Теплота воспламенения дерева $5\cdot 10^4$ Дж/м2.

По закону вина можно найти температуру, при которой выделяется максимальная длина волны, но как можно рассчитать расстояние, на котором произойдет возгорание?

[exitone]

Если считать Землю плоской, то ядерный взрыв излучает в телесном угле $2\pi$(пренебрегаем, что Земля что-то поглощает) . Часть излучения приходится на дерево. Дерево видно в каком-то другом телесном угле (он и задает зависимость от расстояния).

-- 13.01.2014, 22:28 --

Глупость написал в первом предложении. Считайте, что излучение идет во все стороны.

[randy]

какую функцию надо использовать? энергетическую светимость?

[DimaM]

randy в сообщении #813905 писал(а):

По закону вина можно найти температуру, при которой выделяется максимальная длина волны

Можно просто найти температуру, а по температуре - поверхностную мощность излучения. Далее найти мощность, приходящую на деревяшку.

[mihiv]

Считая шар абсолютно черным телом, можно найти полную энергию излучения в нем. А затем по закону $\frac 1 {R^2} $ энергию, попавшую на дерево.

[nikvic]

Откуда задачка?
Если бы была Т возгорания, то всё Ок.
===============
Возможно, надлежит ввести параметр удельная теплоёмкость "поверхности" и рассмотреть процесс роста теплосодержания: по мере роста температуры растёт мощность излучения. Далее - предельный переход к нулю этого параметра.

[randy]

DimaM в сообщении #814106 писал(а):

randy в сообщении #813905 писал(а):

По закону вина можно найти температуру, при которой выделяется максимальная длина волны

Можно просто найти температуру, а по температуре - поверхностную мощность излучения. Далее найти мощность, приходящую на деревяшку.

по закону Вина $\lambda = \frac {0.002898}{T}$ Отсюда температура $T=\frac{0.002898}{0.29 \cdot 10^{-6}}=0.009 \cdot 10^6$ К
Применим закон Стефана-Больцмана для нахождения мощности АЧТ $j=\sigma T^4=5.67 \cdot 10^{-8} \cdot 0.009 \cdot 10^6=0.051 \cdot 10^{-2}$ А зависимость приходящей мощности от расстояния как получить?

-- 14.01.2014, 19:28 --

mihiv в сообщении #814117 писал(а):

А затем по закону $\frac 1 {R^2} $ энергию, попавшую на дерево.

поясните, откуда такая зависимость

-- 14.01.2014, 19:29 --

nikvic в сообщении #814210 писал(а):

Откуда задачка?

из раздела "тепловое излучение"

[Munin]

randy в сообщении #814375 писал(а):

А зависимость приходящей мощности от расстояния как получить?

$\sim R^{-2}$ же...

[randy]

допустим, что это так. но надо же еще учесть поглощательную способность дерева? то есть не $\frac {1}{R^2}$, а $\frac {1}{0.7\cdot R^2}$? то есть какое-то тепло вначале будет поглощаться, не нагревая само дерево.
и радиус огненного шара зачем дан?
вообще, если сверить размерности данной теплоты воспламенения дерева Дж/м^2 и получившейся мощности из закона С-Б, расхождение будет в знаменателе. Это допустимо?
j=Вт/м^2=Дж/(м^2*с)

[nikvic]

randy в сообщении #814384 писал(а):

если сверить размерности данной теплоты воспламенения дерева Дж/м^2 и получившейся мощности из закона С-Б, расхождение будет в знаменателе. Это допустимо?

Вообще-то нет.
Меня удивило, что в условии Дж/м^2, а не мощность/время - как для солнечной постоянной, например.

[randy]

вполне возможно, что в размерности опечатка.
как я понял, для принятия соотношения $j=R^{-2}$ нужно считать, что огненный шар - точка, то есть энергия исходит из самого центра шара, а при отдалении от центра вектора энергии имеют все меньшую плотность. значит на расстоянии $100$ метров мощность будет $j=\frac {0.051 \cdot 10^{-2}}{100^2}$? Или нужно все таки $R$ отсчитывать не от середины шара, а от конца, из-за того, что энергия распространяется на много большее расстояние, чем радиус шара?

[exitone]

Телесный угол в котором видно площадку $\Delta S$, находящуюся на расстоянии $R$ это $\Omega = \frac{\Delta S_\perp}{R^2}$.
Ваше дерево видно в каком-то телесном угле. И часть излучения, на него приходящееся будет отношением этого угла к полному телесному углу, т.е. $\frac{\Omega}{4\pi}$.
А полную мощность излучения Вы уже знаете...

[randy]

exitone в сообщении #814438 писал(а):

Телесный угол в котором видно площадку $\Delta S$, находящуюся на расстоянии $R$ это $\Omega = \frac{\Delta S_\perp}{R^2}$.
Ваше дерево видно в каком-то телесном угле. И часть излучения, на него приходящееся будет отношением этого угла к полному телесному углу, т.е. $\frac{\Omega}{4\pi}$.
А полную мощность излучения Вы уже знаете...

а зачем телесные углы вводить? мы же не знаем $\Delta S$
не проще ли рассчитывать по закону обратных квадратов, как тут предлагали?
приравнять теплоту воспламенения к $\frac {0.051 \cdot 10^{-2}}{R^2}$, и отсюда искать $R$. Только нужно определиться, что вносит коэффициент $0.7$ - поглощательная способность дерева

[exitone]

$j= 0,7 \frac{\Omega}{4\pi}\sigma T^4 4\pi r^2 $ - та мощность, которая приходится на ваше дерево
Вводить $\Delta S$ разумно по той причине, что Вам дана

randy в сообщении #813905 писал(а):

Теплота воспламенения дерева $5\cdot 10^4$ Дж/м2.

Напишите закон сохранения энергии (все величины в джоулях). И поделите на $\Delta S$.

[mihiv]

Мне сначала показалось, что можно действовать таким образом: найти энергию излучения в объеме плазменного шара $U_r=uV$,где $u=\dfrac {4\sigma }cT^4$ - объемная плотность излучения, $V$- объем шара. Тогда максимальное расстояние возгорания было бы равно :

$$R_{max}=\sqrt {\dfrac {0.7U_r}{4\pi q}}, q=5\cdot 10^4\dfrac {\text {Дж}}{M^2} $$

Но оценка показывает, что при $T=10^4K$, объемная плотность излучения еще не очень велика, и большая часть энергии плазмы - это кинетическая энергия массивных частиц: ионов и электронов $\left (\frac 32kT\right )$. Тогда задача усложняется, т.к. нужно знать концентрации электронов и ионов, учитывать диссоциацию молекул и т.д. Следовательно,

$$R_{max}=\sqrt {\dfrac {0.7E}{4\pi q}},$$

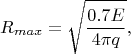
где $E$- энергия излучения + кинетическая энергия частиц (при условии, что основной механизм охлаждения плазмы - излучение).