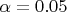Задача из Натана (проверка гипотез)

[eugrita]

При эпидемии гриппа из 200 контролируемых людей однократное заболевание наблюдалось у 181 чел, а дважды болели гриппом 9 чел. Правдоподобна ли гипотеза о том, что в теч эпидемии гриппа число заболеваний отд человека предст с в, подчин биномиальному распределению с числом испытаний $n=2$ ?
-------------------------------------------------------------------------------------
Решение. Возможна проверка по критериям хи-квадрат, Колмогорова
Выбираем ХИ-квадрат. Матожидание числа заболеваний
$\bar{x}=0.995$
так как p не задано, берем ее статист.оценку (сложная гипотеза)
$p=\frac{\bar{x}}{n}=\frac{0.995}{2}=0.4975$
По найденному p считаем теоретические частоты и хи-квадрат
$\Xi^2=1.968$
Проблема в том что в условии задано n=2 и при 1 параметре оцениваемом по выборке $r=1$
$k=n-r-1=2-1-1=0$
Что-то хи-квадрат с 0 степенями свободы нет в табл.
Если брать с 1 ст.свободы то $\Xi^2(1,\alpha)=6$
при $\alpha=0.05$

[provincialka]

Степени свободы определяются не по параметрам проверяемого распределения, а по размеру выборки. Вернее, числу тех групп, на которые вы ее разбили. А у вас какие группы?

[eugrita]

т.е $n=3$?
И правильно считать кол-во ст.свободы=1?

[provincialka]

Да, наверное. Только это очень маленькая степень свободы. Может, попробовать Колмогорова? Правда, он плохо реагирует на не простые гипотезы (можно с учетом этого повысить уровень значимости до 10%)

[--mS--]

eugrita в сообщении #795743 писал(а):

Проблема в том что в условии задано n=2 и при 1 параметре оцениваемом по выборке $r=1$
$k=n-r-1=2-1-1=0$
Что-то хи-квадрат с 0 степенями свободы нет в табл.
Если брать с 1 ст.свободы то $\Xi^2(1,\alpha)=6$
при $\alpha=0.05$

Во-первых, число интервалов группировки при использовании критерия не $2$, а $3$: не болели, болели однажды, дважды. И очень интересно, как у Вас получилось значение $\Xi^2=1.968$?
И никаких $6$ не может получиться у распределения хи-квадрат с одной степенью свободы: это просто квадрат стандартной нормальной случайной величины, и $\mathsf P(\chi^2_1 > 3,8414588207)=2\Phi_{0,1}(-\sqrt{3,8414588207})=0.05$.

-- Ср дек 04, 2013 10:38:56 --

provincialka в сообщении #795755 писал(а):

Может, попробовать Колмогорова? Правда, он плохо реагирует на не простые гипотезы (можно с учетом этого повысить уровень значимости до 10%)

Он плохо реагирует на непростые гипотезы, но ещё хуже - на дискретные распределения. У него от них крышу сносит.

[--mS--]

(Оффтоп)

Кстати, хи - он не кси: $\chi^2$, а не $\Xi^2$.