You are right. Here is an appropriate potential function, which unfortunately is not easy to describe.
Let

and for every
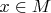
define

as the set of points closest to

.
Define a graph

whose vertices are the elements of

and every vertex
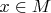
has incident edges

for every

. For each edge, we assign length equal the distance between its endpoints.
Notice that graph

does not depend on a particular partition of

into sets

and

.
Let

be a fixed ordering of the edges of

such that the length of edges does not increase.
Now, define the potential function associated with partition

as

where the coefficient

if the endpoints of edge

are in distinct parts (i.e., one in

and the other in

); otherwise

.
For example, suppose that

and

so that we move

from

to

.
The inequality

implies that

.
The potential here changes as follows:
(i) the coefficient of every edge

for

turns from 1 to 0 (there is at least one such edge);
(ii) the coefficients of edges

(if they present in

) for

turn from 0 to 1.
However, the edges of type (i) are strictly shorter than the edges of type (ii) (since

), and thus edges of type (i) have higher indices, making the potential decrease.