У меня нет под рукой Филиппова, но я бы поступила так. Постараемся найти

из равенств


Сразу хочется поделить равенства на

, тем более оно здесь не может быть равным 0 . Полуучаем
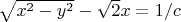

Уединим радикалы:


Теперь видно, что оба решения можно объединить в одно, обозначив свободный член в скобке после

через

или снова через

. Так как знак

произволен, то и константа

произвольна. Впрочем, из построения следует, что она не равна 0, но эти случаи можно проверить отдельно. Итак, первый интеграл приобретает вид

. Знак выбираем так, чтобы правая часть была положительной.
Думаю, дальнейшие действия понятны: избавиться от радикала и выделить полный квадрат.