Отложим пока попытки сделать

двучленом.
Заметим только, что необходимые и достаточные условия, доказанные в предыдущем сообщении представляют равенство нулю квадратичных форм от коэффициентов
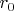
, ...,

.
Для установления закономерностей, хорошо бы иметь программу, приводящую квадратичные формы к каноническому виду.
Вернёмся к оценке числа

с минимальными коэффициентами, где

- идеал, генерированный числами

и

.
Мы показали, что существует

с коэффициентами меньше чем
![$\sqrt[n]{a}$ $\sqrt[n]{a}$](https://dxdy-02.korotkov.co.uk/f/d/7/2/d72b1cb22cd501be6030248b1d393f9e82.png)
по абсолютной величине.
Для этого мы использовали элементарные соображения.
Заметим, однако, что ту же оценку можно получить по теореме Минковского, если вместо

-мерного "шара" рассматривать

-мерный "куб" со стороной
![$2 \sqrt[n]{a}$ $2 \sqrt[n]{a}$](https://dxdy-02.korotkov.co.uk/f/d/3/e/d3e6289e76573f5f40f7fd9ba5de37ee82.png)
.
Кроме элементов идеала

можно рассматривать элементы идеала

, генерированного числами

и

.
Пусть
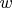
- вычет по модулю

, такой что

по модулю

.
Можно показать, что
![$\beta=r_0+r_1 \sqrt[n]{4}+...+r_{n-1} (\sqrt[n]{4})^{n-1}$ $\beta=r_0+r_1 \sqrt[n]{4}+...+r_{n-1} (\sqrt[n]{4})^{n-1}$](https://dxdy-03.korotkov.co.uk/f/6/b/7/6b765f4ccda24b60beb4e3564c778c2d82.png)
принадлежит идеалу

тогда и только тогда, когда

, ...,

по модулю

.
В самом деле

делится на

(если

).
Значит
![$\beta (w-\sqrt[n]{4})=(r_0 w-4 r_{n-1})+(r_1 w-r_0) \sqrt[n]{4}+...+(r_{n-1} w-r_{n-2}) (\sqrt[n]{4})^{n-1}$ $\beta (w-\sqrt[n]{4})=(r_0 w-4 r_{n-1})+(r_1 w-r_0) \sqrt[n]{4}+...+(r_{n-1} w-r_{n-2}) (\sqrt[n]{4})^{n-1}$](https://dxdy-01.korotkov.co.uk/f/8/9/f/89fae99859eeb9cb54ddb0a5f6c8cece82.png)
делится на

.
Значит

, ...,

по модулю

.
Эти необходимые условия для принадлежности числа

идеалу

являются достаточными, так как из них следует, что

делится на

, следовательно

делится на

, следовательно

делится на

, поскольку число

взаимно-просто с

.
Можно показать, что наборы коэффициентов

, удовлетворяющие этим условиям образуют подгруппу индекса

группы

.
Значит объём фундаментальной области решётки, образованной этой подгруппой равен

.
Согласно теореме Минковского с

-мерным "кубом", существует число

, все коэффициенты
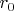
, ...,

которого меньше

по абсолютной величине.
Я затрудняюсь получить этот результат из элементарных соображений.
Имеем:
(20)

.
Все коэффициенты числа

меньше

по абсолютной величине.