Я решил привести полную версию доказательства.
Краткое, альтернативное Эйлерову, доказательство ВТФ для степени 3.
В этой работе мы доказываем, что равенство

невозможно в целых взаимно-простых числах, отличных от нуля.
В доказательстве используется кольцо
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
и его следующие cвойства:
(I) Любой делитель единицы в кольце
![$\mathbb{Z}[j]$ $\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/4/b/d/4bde5ff5237c13d255269f87e9cc8e7982.png)
имеет вид
![$\pm (\sqrt[3]{2}-1)^k$ $\pm (\sqrt[3]{2}-1)^k$](https://dxdy-04.korotkov.co.uk/f/7/8/b/78bb06ca63796785fab44709f8ac4b7b82.png)
, где

-целое число (ссылка 1).
(II) Кольцо
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
содержит все целые алгебраические числа поля
![$\mathbb{Q}[\sqrt[3]{2}]$ $\mathbb{Q}[\sqrt[3]{2}]$](https://dxdy-01.korotkov.co.uk/f/c/4/1/c4166a1e741c55bec053c0ce437e3c0a82.png)
(ссылка 2).
(III) Дискриминант поля
![$\mathbb{Q}[\sqrt[3]{2}]$ $\mathbb{Q}[\sqrt[3]{2}]$](https://dxdy-01.korotkov.co.uk/f/c/4/1/c4166a1e741c55bec053c0ce437e3c0a82.png)
равен -108 (ссылка 2).
Также в доказательстве используется следующие классические теоремы теории алгебраических чисел:
(IV) Существование и единственность разложения идеала в произведение простых идеалов в числовом поле (ссылка 3)
(V) (ссылка 4):
Пусть

- числовое поле cо степенью

расширения

, где

- сигнатура

.
Пусть

- кольцо целых алгебраических чисел поля

.
Пусть

- идеал кольца

.
Тогда существует такой элемент

, что

,
где

- дискриминант поля

.
Лемма 1
-----------
Если

является квадратом целого числа, где

и

- целые числа, то

делится на 3.
Доказательство:
------------------
Предположим

не делится на 3.
Поскольку куб числа не делящегося на

даёт остаток

или
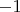
при делении на

, то

даёт при делении на

остаток

, или

. Поскольку квадрат целого числа даёт остаток

,

,

или

при делении на

, то

не является квадратом целого числа, что противоречит условию леммы.
Лемма 2
-----------
Если

и

- взаимно-простые целые числа,

-нечётное положительное число и

, то

.
Доказательство:
--------------------
Предположим, что

.
Тогда
(2.1)

.
Поскольку

, то сомножители в левой части равенства (2.1) - взаимно-просты, и из (2.1) следует, что оба сомножителя являются кубами целых положительных чисел.
Пусть
(2.2)

и

, где

и

- целые положительные числа.
Из равенств (2.2) следует, что

и

, что невозможно, так как

.
Лемма 3
----------
Обозначим
![$j=\sqrt[3]{2}$ $j=\sqrt[3]{2}$](https://dxdy-04.korotkov.co.uk/f/3/8/6/38640a64f5ba47540ae154813c61cb3d82.png)
.
Пусть

и

- целые взаимно-простые числа,

- нечётное число, и

делится на 3.
Тогда

и

не имеют в
![$\mathbb{Z}[j]$ $\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/4/b/d/4bde5ff5237c13d255269f87e9cc8e7982.png)
общих делителей - идеалов.
Доказательство:
--------------------
Предположим, что

и

имеют общий простой делитель: идеал

.
Поскольку

- нечётное число, и

взаимно-просто с

, то существуют такие целые числа

и

, что

.
Поскольку

, то

, следовательно
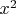
взаимно-просто в
![$\mathbb{Z}[j]$ $\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/4/b/d/4bde5ff5237c13d255269f87e9cc8e7982.png)
с

, и поскольку

делится на

, то
(3.1)

не делится на

.
Поскольку

делится на 3, то
(3.2)

делится на

.
Из (3.1) и (3.2) следует, что

не делится на

и:
(3.3)

не делится на

.
Но

делится на

, что противоречит (3.3).
Лемма 3.1
-------------
Обозначим
![$j=\sqrt[3]{2}$ $j=\sqrt[3]{2}$](https://dxdy-04.korotkov.co.uk/f/3/8/6/38640a64f5ba47540ae154813c61cb3d82.png)
.
Пусть

и

- целые взаимно-простые числа,

- нечётное число и

делится на 3.
Пусть

, где

- ненулевое целое число.
Тогда
![$(x^2-j^2 v) \mathbb{Z}[j]=I^2$ $(x^2-j^2 v) \mathbb{Z}[j]=I^2$](https://dxdy-04.korotkov.co.uk/f/f/a/7/fa76385dd9c804a07370bff7e339991a82.png)
,
где

- некоторый идеал кольца
![$\mathbb{Z}[j]$ $\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/4/b/d/4bde5ff5237c13d255269f87e9cc8e7982.png)
, норма которого равна

.
Доказательство:
--------------------
Имеем:
(3.1.1)

.
Из (3.1.1) следует:
(3.1.2)
![$((x^2-j^2 v)\mathbb{Z}[j])((x^4+j^2 x^2 v+j^4 v^2)\mathbb{Z}[j])=(a \mathbb{Z}[j])^2$ $((x^2-j^2 v)\mathbb{Z}[j])((x^4+j^2 x^2 v+j^4 v^2)\mathbb{Z}[j])=(a \mathbb{Z}[j])^2$](https://dxdy-03.korotkov.co.uk/f/2/4/6/24664376c972aaa84c4295d25021d04382.png)
,
Если какой-либо простой идеал

является делителем идеала
![$(x^2-j^2 v)\mathbb{Z}[j]$ $(x^2-j^2 v)\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/c/2/6/c26caa3ce242c7346d951f6f5ac6a03482.png)
, то идеал
![$(x^4+j^2 x^2 v+j^4 v^2)\mathbb{Z}[j]$ $(x^4+j^2 x^2 v+j^4 v^2)\mathbb{Z}[j]$](https://dxdy-02.korotkov.co.uk/f/5/8/2/5824b8da44a288e9a5f4047a44ebc2da82.png)
не делится на

в силу леммы 3.
Значит идеал

входит в разложение идеала
![$(x^2-j^2 v)\mathbb{Z}[j]$ $(x^2-j^2 v)\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/c/2/6/c26caa3ce242c7346d951f6f5ac6a03482.png)
на простые множители в чётной степени, поскольку

входит в чётной степени в разложение правой части равенства (3.1.2).
Следовательно, идеал
![$(x^2-j^2 v)\mathbb{Z}[j]$ $(x^2-j^2 v)\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/c/2/6/c26caa3ce242c7346d951f6f5ac6a03482.png)
является квадратом некоторого идеала

.
Поскольку норма идеала
![$(x^2-j^2 v)\mathbb{Z}[j]$ $(x^2-j^2 v)\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/c/2/6/c26caa3ce242c7346d951f6f5ac6a03482.png)
равна

, то норма идеала

равна

, что и требовалось.
Лемма 3.2
--------------
Обозначим
![$j=\sqrt[3]{2}$ $j=\sqrt[3]{2}$](https://dxdy-04.korotkov.co.uk/f/3/8/6/38640a64f5ba47540ae154813c61cb3d82.png)
.
Пусть

и

- целые взаимно-простые числа,

- нечётное число и

делится на 3.
Пусть

, где

- ненулевое целое число.
Тогда

,
где

- некоторый делитель единицы в кольце
![$\mathbb{Z}[j]$ $\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/4/b/d/4bde5ff5237c13d255269f87e9cc8e7982.png)
, а

- некоторое число этого кольца.
Доказательство:
---------------------
Согласно лемме 3.1, в кольце
![$\mathbb{Z}[j]$ $\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/4/b/d/4bde5ff5237c13d255269f87e9cc8e7982.png)
, существует идеал

, такой что:
(3.2.1)
![$(x^2-j^2 v) \mathbb{Z}[j]=I^2$ $(x^2-j^2 v) \mathbb{Z}[j]=I^2$](https://dxdy-04.korotkov.co.uk/f/f/a/7/fa76385dd9c804a07370bff7e339991a82.png)
,
(3.2.2)

.
Cогласно (V), существует такое число

, принадлежащее идеалу

, что:
(3.2.3)

,
где

,

,

в силу (III),

в силу (3.2.2).
Значит:
(3.2.4)

,
Вычисление

(коммандой "print 4/3.14*6/27*108^.5" на UBASIC) даёт 2.94..., значит:
(3.2.5)

.
Из (3.2.5) следует:
(3.2.6)

.
Число

является целым алгебраическим числом, потому что из принадлежности числа

идеалу

, следует, что

принадлежит идеалу
![$I^2=(x^2-j^2 v) \mathbb{Z}[j]$ $I^2=(x^2-j^2 v) \mathbb{Z}[j]$](https://dxdy-03.korotkov.co.uk/f/2/9/8/29893de4a147b27d3f4069a1ec2d4c3482.png)
.
Значит
(3.2.7)

является целым числом.
Поскольку

, то:
(3.2.8)

является квадратом рационального числа.
Из (3.2.7) и (3.2.8) следует:
(3.2.9)

является квадратом целого рационального числа.
Из (3.2.6) и (3.2.9) следует:
(3.2.10) либо

, либо

Поскольку

, то:
(3.2.11) либо

, либо

Из (3.2.11) следует:

,
где

- делитель единицы и либо

, либо

, что и требовалось.
Лемма 4
-----------
Если

и

- взаимно-простые целые числа,

-нечётное положительное число и

, то

не является квадратом целого числа.
Доказательство:
--------------------
Предположим:
(4.1)

является квадратом целого числа, где

- наименьшее такое положительное нечётное число,

и

и

- взаимно-простые целые числа.
Обозначим
![$j=\sqrt[3]{2}$ $j=\sqrt[3]{2}$](https://dxdy-04.korotkov.co.uk/f/3/8/6/38640a64f5ba47540ae154813c61cb3d82.png)
.
Из (4.1) и леммы 1 следует, что

делится на 3, и из леммы 3.2 следует:
(4.3)

, где

- делитель единицы в
![$\mathbb{Z}[j]$ $\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/4/b/d/4bde5ff5237c13d255269f87e9cc8e7982.png)
, и

,

и

-целые числа.
Из (I) следует:
(4.4)

, где

-целое число.
Поскольку

- нечётное число, то

, и из (4.1) следует:
(4.5)

Поскольку

и

, то из (4.5) следует:
(4.6)

.
Из (4.3) и (4.6) следует, что

, и из (4.4) следует:
(4.7)

, где

-целое число.
Из (4.3) и (4.7) следует, что либо:
(4.8)

является квадратом в
![$\mathbb{Z}[j]$ $\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/4/b/d/4bde5ff5237c13d255269f87e9cc8e7982.png)
, либо:
(4.9)

является квадратом в
![$\mathbb{Z}[j]$ $\mathbb{Z}[j]$](https://dxdy-01.korotkov.co.uk/f/4/b/d/4bde5ff5237c13d255269f87e9cc8e7982.png)
.
Имеем:
(4.10)

.
Поскольку коэффициент при
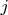
в правой части (4.10) - нечётное число, то (4.9) невозможно, и имеет место (4.8), следовательно:
(4.11)

, где

,

и

-целые числа.
Будем считать, что
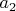
- неотрицательное число (иначе изменим знак у

,

и
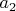
).
Из (4.11) следует:
(4.12)

(4.13)

(4.14)

Все три числа

,

и
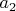
не равны нулю, так как:
если

, то

из (4.13), и левая часть (4.12) обращается в 0, что невозможно;
если

, то

из (4.13), и левая часть (4.14) обращается в 0, что невозможно,
поэтому:
(4.15)

и

;
если

, то

или

из (4.13), что невозможно согласно (4.15).
Поскольку
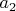
- неотрицательное число, то:
(4.16)

.
Из (4.13) и (4.16) следует:
(4.17)

,

,

,
где

и

взаимно-простые целые положительные числа, и

- целое положительное число.
Из (4.12) и (4.17) получим:
(4.18)

.
Из (4.18) и нечётности

следует:
(4.19)

- нечётное число.
Поскольку

и

- взаимно-простые положительные числа, то из (4.18) и (4.19) следует, что

и

- взаимно-простые положительные числа, и:
(4.20)

для некоторого целого положительного числа
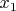
,
(4.21)

является квадратом целого числа.
Из (4.20) и (4.21) следует:
(4.22)

является квадратом целого числа.
Из (4.19) и (4.20) следует:
(4.23)
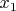
- нечётное целое положительное число.
Из (4.20) и взаимной простоты чисел

и

следует:
(4.24)
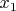
и

- взаимно-простые числа.
Поскольку

- положительное число, то:
(4.25)

Из леммы 2 и (4.18) следует:

, поэтому из (4.20) следует:
(4.26)

Вместе: (4.22), (4.24), (4.23), (4.25) и (4.26) противоречат минимальности

в (4.1).
Теорема А
--------------
Равенство

невозможно в целых взаимно-простых числах, отличных от нуля.
Доказательство:
--------------------
Предположим:
(А.1)

и
(А.2)

,

и

- взаимно-простые целые числа, отличные от нуля.
Поскольку

и

- взаимно-простые числа, то хотя бы одно из них нечётное.
Если

- чётное, поменяем числа в

и

местами.
Если
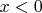
изменим знак чисел в

,

и

на противоположный.
Получим:
(A.3)

- нечётное положительное число.
Из тождества

и (А.1) следует:
(А.4)

является квадратом целого числа.
Обозначим

.
Из (А.2) следует:
(А.5)

и

- взаимно-простые целые числа,
(А.6)

Из (А.4) следует:
(А.7)

является квадратом целого числа.
Вместе (А.7), (А.3), (А.5) и (А.6) вместе противоречат лемме 4.
Ссылки:
1. "Теория Чисел", Боревич, Шафаревич, 1985, Задача 5, страница 125.
2. "Introductory Algebraic Number Theory", Saban Alaca, Kenneth S. Williams, 2004,
страница 153, example 7.1.6.
3. "Algebraic Number Theory", R. Mollin, 1999, стр. 134, Corrollary 3.20.
4. "Algebraic Number Theory", R. Mollin, 1999, стр. 150, Theorem 3.47.
-- Пн окт 14, 2013 20:23:44 --Перед проверкой этого формального доказательства, предлагаю следующее введение (на английском языке):
Recently I have found two simple proofs of FLT for n=3.
They use the ring
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
.
If

then
(1)

,
where

.
The idea is to deduce from (1) that the algebraic number
![$x^2-\sqrt[3]{4} yz$ $x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2382cb9b33d6ed7dbe22cf60fc3d734c82.png)
is a square, more precisely:
(2)
![$x^2-\sqrt[3]{4} yz=u \beta^2$ $x^2-\sqrt[3]{4} yz=u \beta^2$](https://dxdy-04.korotkov.co.uk/f/3/3/7/337a7448aa74280dea662aed7e24381a82.png)
,
where
![$\beta \in \mathbb{Z}[\sqrt[3]{2}]$ $\beta \in \mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-04.korotkov.co.uk/f/b/b/0/bb02b35d9a4f4d214b73c410bd40c36882.png)
, and

is a unit.
Once this is established, then it is not difficult to get a contradiction via infinite descent.
It is similar to Euler's proof, but another number field is used.
The (2) follows from the unique factorization in the Euclidean ring
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
My second proof deduces (2) without using the unique factorization.
The idea is simple: find a number
![$\alpha \in \mathbb{Z}[\sqrt[3]{2}]$ $\alpha \in \mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-02.korotkov.co.uk/f/d/3/0/d30939724b9fb8362cadc8019293cc5c82.png)
, such that

is divided by the
![$x^2-\sqrt[3]{4} yz$ $x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2382cb9b33d6ed7dbe22cf60fc3d734c82.png)
and
![$\alpha^2/(x^2-\sqrt[3]{4} yz)$ $\alpha^2/(x^2-\sqrt[3]{4} yz)$](https://dxdy-03.korotkov.co.uk/f/6/c/f/6cf09e5efb35a5690c7365de2d8a2aa782.png)
has a small norm.
It turns out that the last number may have small norm indeed: less than 9.
Then the norm of it can be either 1 or 4, and (2) easily follows.
The method can be used to prove FLT for other concrete

as well.
It is easy to get such

because

belongs to

, where

is the ideal of norm

, generated by

and
![$x^2-\sqrt[3]{4} yz$ $x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2382cb9b33d6ed7dbe22cf60fc3d734c82.png)
.
We know from the theory of algebraic numbers, that there is an

,
such that

, where

is easily calculated constant, that turns to be less than 3.
Then
![$N(\alpha^2/(x^2-\sqrt[3]{4} yz))<(3 a)^2/a^2=9$ $N(\alpha^2/(x^2-\sqrt[3]{4} yz))<(3 a)^2/a^2=9$](https://dxdy-02.korotkov.co.uk/f/1/e/e/1eedcd2bcf9de27db7bfa454c19099a782.png)
.
This proof is shorter and easier than that of Euler and Kummer.
---------------------------------------------------------------------------
Now I'll explain how to get contradiction from (2).
We may assume, that

is odd, otherwize take

to play the role of

.
Units in the ring
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
have the form:
![$u=\pm(\sqrt[3]{2}-1)^k$ $u=\pm(\sqrt[3]{2}-1)^k$](https://dxdy-02.korotkov.co.uk/f/5/8/2/5825772ad8eed942803d26e1a15cc5c882.png)
, where

is integer.
Therefore, from (2) follows, that either
(3)
![$x^2 - \sqrt[3]{4} y z=\beta_1^2$ $x^2 - \sqrt[3]{4} y z=\beta_1^2$](https://dxdy-01.korotkov.co.uk/f/c/5/2/c52bc3477bfb3e2236f45cdab33b6fa382.png)
or
(4)
![$(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} y z)=\beta_2^2$ $(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} y z)=\beta_2^2$](https://dxdy-03.korotkov.co.uk/f/2/5/b/25b6bd95b7de8de534075a00dd65b1e882.png)
where

and

belong to the ring
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
.
However (4) is impossible, because the coefficient at
![$\sqrt[3]{2}$ $\sqrt[3]{2}$](https://dxdy-03.korotkov.co.uk/f/e/0/d/e0db901a13e9b18861b1a7edb00bdf4a82.png)
turns out to be odd in the left part and even in the right part of (4).
Therefore (3) takes place, that is:
(5)
![$x^2-\sqrt[3]{4} yz=(a_0+a_1 \sqrt[3]{2}+a_2 (\sqrt[3]{2})^2)^2$ $x^2-\sqrt[3]{4} yz=(a_0+a_1 \sqrt[3]{2}+a_2 (\sqrt[3]{2})^2)^2$](https://dxdy-02.korotkov.co.uk/f/5/b/5/5b51092e9954b698138ffbe0712498e582.png)
,
where

,

and
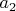
are integers.
From (5) we get:
(6)

(7)

(8)

It follows, that all three numbers

,

and
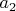
are not zero.
We may assume, that

, otherwise change sign of all three numbers.
It follows from (7) that

,

,

,
where

and

are relatively prime positive integers and

is a positive integer.
Now it follows from (6) that:
(9)

From (9) it follows that

is a square, that is

, and

is a square, that is:
(10)

is a square
It can be shown, that

(a separate lemma).
Then from (9) it follows, that

, that is

and we've got the infinite descent.