Плетение косичек

[Dave]

Пусть $n$ - натуральное число. Косичкой в направлении $i$, $i=\overline {1,n}$ называется подмножество $\mathbb R^n$, равное декартовому произведению луча вида $x_i \geqslant a$ на некоторое ограниченное множество с непустой внутренностью. К примеру, при $n=3$, множество $\{(x_1,x_2,x_3) \mid x_1^2+x_3^2<1, x_2 \geqslant -4\}$ - косичка в направлении $2$.
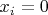
При каких $n$ всё $\mathbb R^n$ можно разбить на косички так, чтобы при любом $i=\overline {1,n}$ косички в направлении $i$ при проекции на гиперплоскость $x_i=0$ заполняли всю эту гиперплоскость? Ответ обосновать.