provincialkaВот так

? А у этого уравнения непонятно как искать корни.
Спасибо за совет, сейчас попробую так сделать.
-- 11.09.2013, 22:17 --provincialkaБольшое спасибо, Ваш способ намного проще.
По условию

.
Тогда:
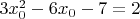
, то есть

и

.
Получаем две касательные:

и

.
Первая не подходит по условию, тогда

.
Но не могу понять, почему не получается моим способом...