Не знаю, может я что-то делаю неправильно, но у меня получились следующие корни из

:

Как находил:

. Если нарисовать, то видно, что

. Тогда первый корень равен
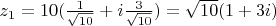
. Ну а второй корень это такой же только с противоположным знаком (так как прибавляется только

).
И при подстановке в корни исходного уравнения тем не менее получается неверно.
