Читаю Рубакова, введение в классическую теорию полей. И тут есть одна задачка, которая ввела меня в тупик. Задачка, вообще говоря по математике, но т.к. я физик, плюс из книжки физической взято, то выкладываю ее в этом разделе. Итак условие:
Описать центр группы

и показать, что он изоморфен

.
Связанные определения и обозначения стандартны, но на всякий случай:
Центр группы
(Оффтоп)
Центром группы
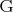
называют множество ее элементов

, таких что

коммутирует с любым ее элементом

:


(Оффтоп)

, специальная унитарная группа -- группа унитарных матриц

, т.е. матриц таких, что ее эрмитово сопряжение равно обратной:


(Оффтоп)

-- группа целых чисел по модулю

, где групповое умножение есть сложение чисел по модулю

Откуда подойти я даже не знаю. Хотел подойти с той стороны, что

-- комплексное расширение

, которая есть группа вращений в

-мерном пространстве. Но построить общий вид

по аналогии мне не удалось. Вроде

-- некоммутативна в случае размерности больше двух, тогда для нее центром будет одна лишь единичная матрица. Но как это показать аккуратно математически я не приложу ума. Да и потом, если центр - это лишь единичная матрица, то очевидно, что он не изоморфен

.
И подскажите еще одно, для группы

можно любую матрицу представить как комбинацию поворотов в плоскостях, заменяя соответствующие элементы на подобие:

Тогда итоговая матрица поворота, т.е. элемент

будет произведением таких матриц. Можно ли как-то подобным образом представить элемент

?