Аппроксимация, поиск аналитической формулы

[mathncm]

Здравствуйте! Помогите пожалуйста с поиском аналитической формулы.
Постановка:
Необходимо получить формулу $F(x_{1},x_{2},x_{3},x_{4},....x_{m})=y$
Для набора данных в объеме $ 1\leq j\leq m, 4 \leq m \leq 11$
$x_{i,1}x_{i,2}x_{i,3}x_{i,4} x_{i,m}y_{i}$
...
$x_{n,1}x_{n,2}x_{n,3}x_{n,4} x_{n,m}y_{n}$
$1\leq i\leq n$
Особенности данных:
$x_{i,j}$ - может принимать от 1 до 20 разных значений с определенным шагом.
Пусть $c_{j} = |x_{i,j}|$ - количество различных значений $x_{i,j}$ для $j$-той независимой.
например $x_{1,1} = {2, 4, 8, 10,...,2 \cdot c_{1}}$
или $x_{1,2} = {0.1, 0.2, 0.3,...0.1 \cdot c_{2}}$
и т.д. (значения могут быть от 1.e-9 до 1.e+9).
Тогда данные составляются путем комбинации всех вариантов $x_{i,j}$, то есть получается $n = \prod_{i=1}^{m}c_{i}$ (n - объем данных, m - количество независимых параметров).
Для каждой $i$-той комбинации вычисляется $y_{i}$ (сложные вычисления).
Так и получается набор данных,
$x_{i,1}x_{i,2}x_{i,3}x_{i,4}x_{i,m}y_{i}$
...
$x_{n,1}x_{n,2}x_{n,3}x_{n,4}x_{n,m}y_{n}$
который может составлять гигабайты.

Способ решения:
Способ состоит в использовании "Polynomial curve fitting", а точнее функция p = polyfit(x,y,nFits) в MATLAB, где $x,y$-вектор, nFits степеней.
В итоге если nFits = 1, то функция находит коэффициенты $a,b$ такие, что $F(x) = a \cdot x + b$ (при вычислении используется nFits = 4).

Метод состоит в том, чтобы "сжимать" данные по каждому из параметров.
Например:
Пусть исходные данные состоят из 4х независимых

$x_{i,1}x_{i,2}x_{i,3}x_{i,4} y_{i}$
...
$x_{n,1}x_{n,2}x_{n,3}x_{n,4} y_{n}$
$m = 4$
Тогда находим все различные комбинации без последнего $x_{i,4}$:
$x_{k,1}x_{k,2}x_{k,3}=A_{k}$
всего таких комбинаций будет $n_{1} = \prod_{i=1}^{m - 1}c_{i}$, $1\leq k \leq n_{1}$
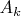
и каждой комбинации $A_{k} $ будет соответствовать $c_{m}$ разных значений $x_{i,m}$ и $y_{i}$ из исходного набора.
Теперь для этих ($x_{i,m}$ и $y_{i}$ ) данных найдем коэффициенты с помощью polyfit().
В результате построим новый набор данных, который будет в $c_{m}$ раз меньше исходного.
$x_{i,1}x_{i,2}x_{i,3} a_{i} b_{i} $
...
$x_{n_1,1}x_{n_1,2}x_{n_1,3} a_{n_1} b_{n_1} $
теперь в качестве y, уже имеет два значения a,b, для каждого ищется новые коэффициенты, далее происходит замена аналогичным образом.
И так "сжатие" выполняется на $c_{m-1},c_{m-2},...,c_1$.
В конце концов, остается только $2^4$ коэффициентов, из которых составляется формула по вычисленным коэффициентам a,b,c,d,...,n,o,p:
$F(x_{1},x_{2},x_{3},x_{4}) = (((a \cdot x_{1}+ b) \cdot x_{2}+ c \cdot x_{1}+ d) \cdot x_{3} + (e \cdot x_{1}+ f) \cdot x_{2} + g \cdot x1 + h \cdot x_{4}+ ((i \cdot x_{1}+ j) \cdot x_{2} + k \cdot x_{1}+ l) \cdot x_{3} + (m \cdot x_{1} + n) \cdot x_{2} + o \cdot x_{1} + p$

Эксперименты:
Вычисления проводились для структур из 4-11 параметров по 100-200 мб данных, на некоторых структурах данные восстановленные по формуле почти полностью совпадают с исходными (могу вставить рисунки). Но есть проблемы.

Проблема:
Главная проблема заключается в том, что формулы получаются слишком длинные,
количество коэффициентов вычисляется по формуле $(p+1)^s$ s - количество параметров, p - полиномы, то есть для 4 полиномов и 6 параметров будет 15625 коэффициентов, если составить формулу, то она будет занимать $\frac{(4+1)^{6}\cdot8}{1024}$ то есть ~ 122 килобайта.
Для 11 параметров и 4 полинома (макс тест) ~ 372 Mb.

Также на некоторых структурах появляются сильное расхождение с реальными данными, что неприемлемо.

Увеличение полиномов повышает точность, но количество коэффициентов становится еще больше.

Подскажите, пожалуйста, что еще можно применить?
Спасибо.