помогите решить 2 системы интегральных ур-ний.

[Touol]

Предупреждение: Гипотезы и идеи изложенные в статье могут как и быть физической реальностью так и легко не иметь никакого отношения к физической реальности. Это просто один из возможных вариантов обобщение квантовой физики. Таких вариантов можно придумать довольно много. На данный момент этот вариант не является полноценной теорией. Полноценная теория включает в себя эксперименты, которые могут ее опровергнуть или подтвердить. Надеюсь, что рано или поздно теория дойдет до экспериментов. Буду рад, если вы захотите помочь в развитии нижеизложенных идей до полноценной теории.
Просьба: Как-то не верю, что глупые люди вообще существуют. Даже, тех кого считают глупыми, опасаюсь больше чем, тех кого считают умными. Неизвестно чего от них ждать. Позиционирование себя как умного помогает мне преодолевать лень и напрягать мозги, развивать их . С искренним уважением отношусь к тем кто желает развиваться и разбираться в не такой уж и сложной но все равно непростой квантовой теории . Надеюсь, что это уважение будет взаимным.

whiterussian:

Не так уж и много. Не поленитесь оформить тему по правилам.

== Введение ==
Со времен Бора и Эйнштейна ведутся споры вокруг физического смысла волновой функции (ВФ) в квантовой механике (КМ). Бор утверждал, что квадрат ВФ являтся вероятностью. Вероятностью $P$ найти частицу в объеме $\Delta V$.
: $P(\Delta V)= \int_{V}^{V+\Delta V}{\psi^\ast(\bar x)\psi(\bar x)d\bar x} $. (1)

Эксперименты подтверждают эту формулу. Действительно вероятность найти частицу в объеме пр-ва равна квадрату ВФ. Эйнштейн возражал "Бог не играет в кости. Случайность результата измерений объясняется по другому". В качестве объяснения случайности рез-та, выдвигались различные гипотезы. В основном, что у ВФ есть скрытые параметры, которые определяют измериться (появиться) ли частица в данной области пр-ва, либо появиться в какой-то другой области. Эксперименты по парадоксу Эйнштейна-Подольского-Розена опровергают существование у ВФ скрытых параметров. На данный момент трактовка Бора ВФ признается большинством физиков.

Но для объяснения случайности измерений есть еще одна не рассмотренная возможность. Случайность измерений свойство не ВФ, а измерителей параметров квантовых частиц. В статье я попытаюсь описать эту возможность.

== Некоторые измерители квантовых частиц ==


На рисунке схематично изображены измерители координат: фотоумножитель и фотобумага, измеритель траектории: камера Вильсона, и стекло которое не является измерителем. Во всех случаях квантовая частица ведет себя по разному. Для измерителей координат поглощается в малой, почти точечной области пр-ва. Для измерителя траектории заряженная частица оставляет трек некоторой ширины состоящий из капелек жидкости (или пузырьков газа). В случае стекла ВФ фотона как и до стекла, так и в стекле, так и после стекла представляет протяженную в пр-ве волну.

Во всех случаях мы получаем разное поведение частиц. Однако '''как и стекло так и измерители являются квантового-механическими системами'''. И должны описываться одинаковым образом. '''Независимо являются они измерителями или нет'''.

== В чем разница между стеклом и измерителями? ==
Все измерители, в отличии от стекла, находятся в состоянии неустойчивого равновесия. Частица энергией $\Delta U_1$ попадая в измеритель вызывает переход КМ системы измерителя, из состояния локального минимума энергии в состояние глобального минимума энергии, с выделением энергии $\Delta U_2$ которая как раз и доносит до нас, что частица появилась в измерителе.



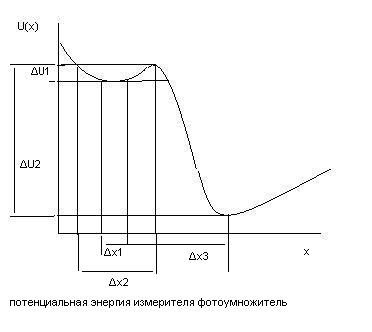
Для стекла, если атом поглотит фотон, с энергией $\Delta U_1$, то через некоторое время он испустит фотон с такой же энергией $\Delta U_2=\Delta U_1$ как и у поглощенного. Этим стекло и отличается от измерителей.



Рассмотрим отражение от стекла и фотоумножитель в формализме фейнмановского интеграла по путям.

== Отражение от стекла и фотоумножитель в формализме фейнмановского интеграла по путям ==


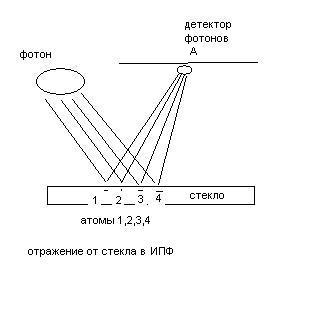
В случае отражения от стекла, для расчета амплитуды вероятности обнаружить фотон на детекторе, можно применить метод интеграла по путям Фейнмана (ИПФ). Фотон попадая на стекло может отразиться допустим от атомов 1,2,3,4. Амплитуда вероятности обнаружить фотон детекторе выразиться как сумма амплитуд прохождения фотона по путям 1,2,3,4.
* $~A=A_1 + A_2+A_3+A_4$ (2.1)

В случае фотоумножителя, фотон может поглотиться электроном либо в окрестности точки 1, либо в окрестности точки 2 и т.д. Выбитый фотоном электрон может придти на экран с точек 1,2,3,4 (точки расположены достаточно далеко от друг друга). По аналогии со стеклом можно было бы ожидать, что амплитуда обнаружить электрон в окрестности точки A, будет также суммой амплитуд путей 1,2,3,4. Но на самом деле, проводя эксперименты мы обнаружим, что электрон проходит либо по пути 1, либо по пути 2, либо по пути 3, либо по пути 4.
Амплитуда вероятности найти фотон в точке A, выразиться по формуле:
* $A=A_1 \vee A_2 \vee A_3 \vee A_4$ (2.2)

Для стекла и фотоумножителя есть 2 различия:
# В точку A для стекла приходит фотон, в фотоумножителе приходит электрон. Пока пренебрежем этой разницей.
# Для стекла $~\Delta U_2=\Delta U_1$, а в фотоумножителе $~\Delta U_2 >> \Delta U_1$.

Случаи 2.1 и 2.2 можно объединить введя некоторую функцию Гаусса с параметром $~\sigma=\frac{E_f-\Delta U_1}{\Delta U_2-\Delta U_1}$. [[w:Нормальное распределение]]
* $f(x_2-x_1) = B e^{ -\frac{(x_2-x_1)^2}{2\sigma^2} }$ (2.3)

$~E_f$ энергия падающего (начального) фотона. $~B$ нормировочный коэффициент, для нормального распределения $B=\tfrac{1}{\sqrt{2\pi\sigma^2}}\;$.

Амплитуда вероятности в точке A запишем в виде:

* $A=(A_1f(x_1-x_1)+A_2f(x_2-x_1)+A_3f(x_3-x_1)+A_4f(x_4-x_1)) \vee $
$(A_1f(x_1-x_2)+A_2f(x_2-x_2)+A_3f(x_3-x_2)+A_4f(x_4-x_2)) \vee $
$(A_1f(x_1-x_3)+A_2f(x_2-x_3)+A_3f(x_3-x_3)+A_4f(x_4-x_3)) \vee $

$~(A_1f(x_1-x_4)+A_2f(x_2-x_4)+A_3f(x_3-x_4)+A_4f(x_4-x_4))$ (2.4)

В случае стекла $~E_f \not = \Delta U_1$, $\Delta U_2-\Delta U_1 \to 0$. $~\sigma \to \infty$. Функция $~f(x_2-x_1)$ переходит в константу и все четыре варианта дают одинаковый результат.
* $~A=$
$~(A_1f(x_1-x_1)+A_2f(x_2-x_1)+A_3f(x_3-x_1)+A_4f(x_4-x_1)) = $
$~(A_1f(x_1-x_2)+A_2f(x_2-x_2)+A_3f(x_3-x_2)+A_4f(x_4-x_2)) = $
$~(A_1f(x_1-x_3)+A_2f(x_2-x_3)+A_3f(x_3-x_3)+A_4f(x_4-x_3)) = $

$~(A_1f(x_1-x_4)+A_2f(x_2-x_4)+A_3f(x_3-x_4)+A_4f(x_4-x_4))$

В случае фотоумножителя $~E_f \approx \Delta U_1$, $~\Delta U_2-\Delta U_1 >> 0$. $~\sigma \to 0$.
Функция $~f(x_2-x_1)$ переходит в дельта-функцию. $~f(x_2-x_1) = 1$ при $~x_2=x_1$ и равно 0 в остальных случаях. Формула 2.4 переходит в формулу 2.2.

Примечание. Формула получена для нерелятивистских частиц. В релятивистской КМ вводиться принцип причинности. Когда $~f(x_2-x_1)$ переходит в дельта-функцию она совершенно аналогична дельта-функции в релятивистской КМ.

== Случайность результата измерений ==
Почему результат измерения случаен? Функция 2.4 в пределе измерений сильно зависит от $~E_f \approx \Delta U_1$.
Нужна другая нормировка. При $~\Delta U_2-\Delta U_1 >> 0$ и $~E_f \not = \Delta U_1$ возможно стоит функцию занулять. Или надо сперва с камерой Вильсона разобраться :).

Для $~E_f \not = \Delta U_1$ поглощение фотона электроном с вылетом менее вероятно. При В результате тепловых и квантовых флуктуаций энергия электронов в металле флюктуирует (изменяется). Вместе с ней флуктуирует нужная для выхода из металла энергия $~\Delta U_1$. Из металла вылетит первый электрон для которого энергия фотона и работа выхода совпадут.
Слишком упрощенно. Но где-то приблизительно в этом направлении. Сравнить с формулами фотоэффекта Эйнштейна.

Для фотобумаги возможно появиться зависимость вероятности поглощения фотонов галогенидом серебра от размеров кристаллов галогенида серебра.

== Выводы ==
В статье феноменологически объединяется детекторы координат и стекло в едином описании. Сделана попытка объяснить случайность рез-тов измерений. При детальном разборе может вылезти достаточно много противоречий, но надеюсь они устранимы в дальнейшей проработке.

Сильная сторона феноменологической модели квантовых измерений в описании процесса измерений. Насколько я знаю, до сих пор сам процесс измерения в КМ не описывался (не объяснялся). Слабость в том, что пока модель описывает только два случая. Нужно расширять описание.

В основу модели легли следующие идеи:
# как и стекло так и измерители являются квантового-механическими системами. И должны описываться одинаковым образом. Независимо являются они измерителями или нет.
# Объединить возможно, если допустить формулу 2.4 с функцией Гаусса. Эта функция некоторый аналог принципа причинности.

В работе следующие идеи:
# Вместо функции Гаусса использовать распределения для бозонов и фермионов. Принцип (анти)коммутативности на массовой пов-ти.
# Результаты не слишком изменяться, если задавать $~\sigma^2=\frac{E_f-\Delta U_1}{\Delta U_2-\Delta U_1}$.
# Как известно волновой пакет частицы быстро расплывается. При измерениях и при взаимодействиях вообще, волновой пакет должен сжиматься. Сжатие волнового пакета эквивалентно принципу энтропии. То есть необратимости времени.

[Touol]

Даны 2 системы интегральных ур-ний:
1)

\begin{cases}\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt+\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=1\\\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt +\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=0 \end{cases}

2)

\begin{cases}\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt)+\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=1\\\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt+\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=\frac{1}{2}\\\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt+\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=0 \end{cases}

где $V_A$ и $V_B$ 2 произвольных не пересекающихся объема пространства.
надо найти $f(x,y,z,t)$ для первого и второго случая.

Возникают в черновике статьи Квантовые измерения или «Я не верю, что бог бросает кости»

(Оффтоп)

Статью обсуждать здесь мне не надо. Модераторы вроде против. Статья чтоб было понятно зачем.

[myhand]

Touol в сообщении #742651 писал(а):

Даны 2 системы интегральных ур-ний:
1)

\begin{cases}\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt+\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=1\\\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt +\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=0 \end{cases}

Тут задачу можно для начала свести к системе линейных уравнения. Она, очевидно, не совместна (т.е. решений - нет).

Touol в сообщении #742651 писал(а):

2)

\begin{cases}\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt)+\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=1\\\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt+\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=\frac{1}{2}\\\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt+\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=0 \end{cases}

Та же петрушка. Только это еще и переопределенная (два неизвестных, три уравнения) система линейных уравнений.

Мораль. Закончите-ка первый курс университета/института, а? А квантовую механику будете изобретать позднее.

[Touol]

myhand в сообщении #742668 писал(а):

Тут задачу можно для начала свести к системе линейных уравнения. Она, очевидно, не совместна (т.е. решений - нет).

Touol в сообщении #742651 писал(а):

где $V_A$ и $V_B$ 2 произвольных не пересекающихся объема пространства.

Это система не 2 ур-ний, а система бесконечного числа ур-ний! $V_A$ и $V_B$ мы можем менять как угодно и двигать и расширять и сжимать. Главное что они не пересекаються.

-- Ср июл 03, 2013 01:14:21 --

myhand в сообщении #742668 писал(а):

Тут задачу можно для начала свести к системе линейных уравнения

Каким образом свести?

-- Ср июл 03, 2013 01:22:52 --

myhand в сообщении #742668 писал(а):

Только это еще и переопределенная (два неизвестных, три уравнения) система линейных уравнений

С какой такой стати? Неизвестная функция. У функции вообще говоря бесконечное число значений. В каждой точке пространства-времени свое значение.

-- Ср июл 03, 2013 01:50:54 --

$\begin{cases}\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt+\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=1\\\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt +\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dVdt=0 \end{cases} $

$f(x,y,z,t)=X(r)T(t)$

$(\int_{V_A}X(r)dV+\int_{V_B}X(r)dV)\int_{t}^{t+\Delta t}T(t)dt=1$

$(C_A+C_B)C_t=1$
$(C_A+C_B)C_t=0$

$(C_A+C_B)=0$ $C_A= - C_B$

гипотеза $f(x,y,z,t)=X(r)T(t)$ не работает!

$f(x,y,z,t)=f(wt-kr)$ волна. Нужно использовать преобразование Фурье!

[Munin]

myhand в сообщении #742668 писал(а):

Мораль. Закончите-ка первый курс университета/института, а? А квантовую механику будете изобретать позднее.

Полностью присоединяюсь. Интегральными уравнениями ваши каракули то, что вы понаписали, не является.

-- 02.07.2013 23:03:11 --

Touol в сообщении #742674 писал(а):

Каким образом свести?

Обозначим $\mathcal{A}=\int_{V_A}\int_{t}^{t+\Delta t}f(x,y,z,t)dV\,dt,$ и, соответственно, $\mathcal{B}=\int_{V_B}\int_{t}^{t+\Delta t}f(x,y,z,t)dV\,dt.$ Получаем:
$\begin{cases}\mathcal{A}+\mathcal{B}=1\\\mathcal{A}+\mathcal{B}=0\end{cases}$
Дальше всё должно быть очевидно даже такому двоечнику, как вы.

[Touol]

Я уже понял. спасибо :) допустил косяк. прозевал предельный переход :(.

[Munin]

Ещё одна бессмысленная фраза.

Почитали бы вы учебники, а?

А то знаете, многие впадают в экстаз от того, что интернет позволяет писать тексты с формулами и графиками, и выкладывать их в публичный доступ, но на самом деле смысла-то в таких текстах не больше, чем если бы вы что-то написали на бумажке, и приклеили жвачкой к стене вуза. Высокопарное слово "статья" к этим каракулям не относится. Когда (если) вы вырастете в человека разумного, вы этого сами стесняться будете.

[myhand]

Да уж. Боюсь, в опубликованных формулах нет и намека на предельный переход, после которого они становятся непротиворечивыми.

[Touol]

$\begin{cases}\lim_{t_{A} \to t}{\int_{V_A}\int_{t_A}^{t_A+\Delta t}f_{1}(x,y,z,t,t_A)dVdt_{A}}+\lim_{t_{B} \to t}{\int_{V_B}\int_{t_B}^{t_B+\Delta t}f_{1}(x,y,z,t,t_B)dVdt_{B}=\frac{n}{N} \Delta t V_{1}}\\\lim_{t_{A} \to t}{\int_{V_A}\int_{t_A}^{t_A+\Delta t}f_{2}(x,y,z,t,t_A)dVdt_{A}}+\lim_{t_{B} \to t}{\int_{V_B}\int_{t_B}^{t_B+\Delta t}f_{2}(x,y,z,t,t_B)dVdt_{B}=\frac{m}{N} \Delta t V_{2}} \end{cases}$

n, m , N целые числа.
При $\Delta t \to 0$. $N \to 1$, $n \to 1$ и $m \to 0$. И $f_1 \to f_2$

такая система совместима?

[myhand]

"Такая система" в этом пределе сводится к двум идентичным бессодержательным тождествам.

[Munin]

То же нет, по тем же причинам, только замена переменных другая.
А, нет, эта система - ещё и вообще бессмысленная.

[Touol]

$\lim_{t_{A} \to t}{\int_{V_A}\int_{t_A}^{t_A+\Delta t}f(x,y,z,t,t')dVdt'}$ -квантовая вероятность. Ее суммировать нельзя. Можно суммировать до предела.
$ \begin{cases}\lim_{t_{A} \to t}{\lim_{t_{B} \to t}{(\int_{V_A}\int_{t_A}^{t_A+\Delta t}f_{1}(x,y,z,t,t')dVdt'}+\int_{V_B}\int_{t_B}^{t_B+\Delta t}f_{2}(x,y,z,t,t')dVdt')=\frac{n}{N} \Delta t V_{1}}\\\\lim_{t_{A} \to t}{\lim_{t_{B} \to t}{(\int_{V_A}\int_{t_A}^{t_A+\Delta t}f_{3}(x,y,z,t,t')dVdt'}+\int_{V_B}\int_{t_B}^{t_B+\Delta t}f_{4}(x,y,z,t,t_B)dVdt)=\frac{m}{N} \Delta t V_{2}}\\\\lim_{t_{B} \to t}{\lim_{t_{A} \to t}{(\int_{V_A}\int_{t_A}^{t_A+\Delta t}f_{5}(x,y,z,t,t')dVdt'}+\int_{V_B}\int_{t_B}^{t_B+\Delta t}f_{6}(x,y,z,t,t')dVdt')=\frac{n}{N} \Delta t V_{1}}\\\\lim_{t_{B} \to t}{\lim_{t_{A} \to t}{(\int_{V_A}\int_{t_A}^{t_A+\Delta t}f_{7}(x,y,z,t,t')dVdt'}+\int_{V_B}\int_{t_B}^{t_B+\Delta t}f_{8}(x,y,z,t,t')dVdt')=\frac{m}{N} \Delta t V_{2}}\end{cases}$

n, m , N целые числа. При $\Delta t \to 0$, $N \to 1$, $n \to 1$ и $m \to 0$.

$f_{1} \to f_{2} \to f_{3} \to f_{4} \to f_{5} \to f_{6} \to f_{7} \to f_{8}$???

Что-то похожее на правду есть?

-- Чт июл 04, 2013 10:34:28 --

В условиях квантового измерения, существует неустойчивость решений ур-ния Шредингера относительно малых изменений начальных условий задачи Коши. Такая, что если при начальных условиях $\phi_1(x,t)$ результат измерения равен 1 (фотон поглотился на одном определенном кристаллике соли серебра), то, при каком-то малом изменении начальных условий $\phi_2(x,t)=\psi(x,t)+\varepsilon\chi(x,t)$, результат измерения равен 0 (фотон не поглотился на этом кристаллике). При этом P отношение числа решений с результатом измерения 1 к числу решений с результатом 0 равно интегралу от квадрата модуля ВФ на измерителе.
$ P=\int_{V}{|\phi_1(x,t)|^2dV} \approx \int_{V}{|\phi_2(x,t)|^2 dV}=\int_{V}{|\phi_1(x,t)|^2 dV}+o(\varepsilon)$

Я предполагаю, что гипотеза справедлива.

$\int_{V_A}\int_{t_A}^{t_A+\Delta t}f(x,y,z,t,t')dVdt'$- статсумма всех решений приводящих к определенному результату.

[Touol]

Touol в сообщении #743084 писал(а):

статсумма всех решений приводящих к определенному результату.

Очень криво сказано. Сейчас еще буду разбираться со статсуммой.

[Munin]

Какой смысл писать кучу значков без малейшего понимания, что они означают, и как используются?

-- 04.07.2013 14:36:03 --

Touol в сообщении #743084 писал(а):

В условиях квантового измерения, существует неустойчивость решений ур-ния Шредингера относительно малых изменений начальных условий задачи Коши.

Это чистый незамутнённый бред. "Условия квантового измерения" и "решение уравнения Шрёдингера" - несовместимые между собою вещи.

И к слову, самое позорное: ВФ измерителя - это ни в коем случае не $\Psi(x,t).$ Это показывает, что вы учебник квантовой механики даже не открывали.

[Touol]

Munin в сообщении #743157 писал(а):

ВФ измерителя - это ни в коем случае не $\Psi(x,t).$

.

Это почему? Нигде такого не читал. В 2 словах можете объяснить?

-- Чт июл 04, 2013 18:39:12 --

Ясно, что зависит от координат многих частиц. Записал упрощенно. Здесь просто ВФ измерителя. Ничего кроме того, что измерителю можно приписать ВФ.

-- Чт июл 04, 2013 19:30:25 --

[url]

Munin в [url=http://dxdy.ru/post743157.html#p743157]сообщении #743157[/url] писал(а):

"Условия квантового измерения" и "решение уравнения Шрёдингера" - несовместимые между собою вещи

[/url]

Сложный вопрос. Думаю многие ломали голову, что происходит при измерениях. Есть еще и ур-ние Дирака. Здесь это просто гипотеза. Гипотеза, что при четко заданной ВФ можно найти результат.
Странно :). Я отолкнулся от нее. Сказал, что нам просто неизвестны начальные данные. И стал исследовать, что нам известно. Что о начальных данных можно узнать. На начальные данные и составлены ур-ния.
О начальных данных можно сказать только их вероятность.
Вы правы измерения и ур-ние Шредингера несовместимы.
Сейчас я думаю, что ур-ния Шредингера, Дирака это ур-ния на вероятность начальных данных. Исходя из них мы делаем предсказания о будущем.