Спектр треугольной функции

[Babeuf]

Здравствуйте.
Никак не могу разобраться с ДПФ, для треугольной функции.
Задаю массив на 80 значений для функции на отрезке $[0,..,0.00001]$:
$triangle_i=10\cdot|{2(2\nu_gt_i-{\operatorname{floor}}(2\nu_gt_i+\frac{1}{2}))|\cdot{\operatorname{sgn}}(\sin(2\pi\nu_gt_i))$
Где:
$t_i$ — массив для отсчётов по времени размерностью 80.
$400$ кГц — частота дискретизации.
$\nu_g=100$ кГц
${\operatorname{floor}}$ — функция извлечения целой части вещественного числа; округление до ближайщего целого в меньшую сторону.
Получаю:


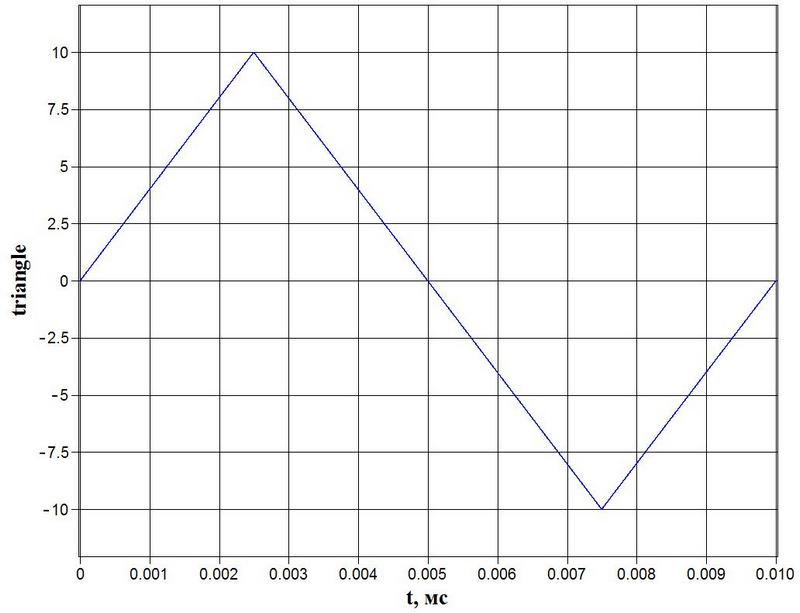
Раскладывая сигнал $triangle$ в спектр, с помощью ДПФ получаю следующую картину:

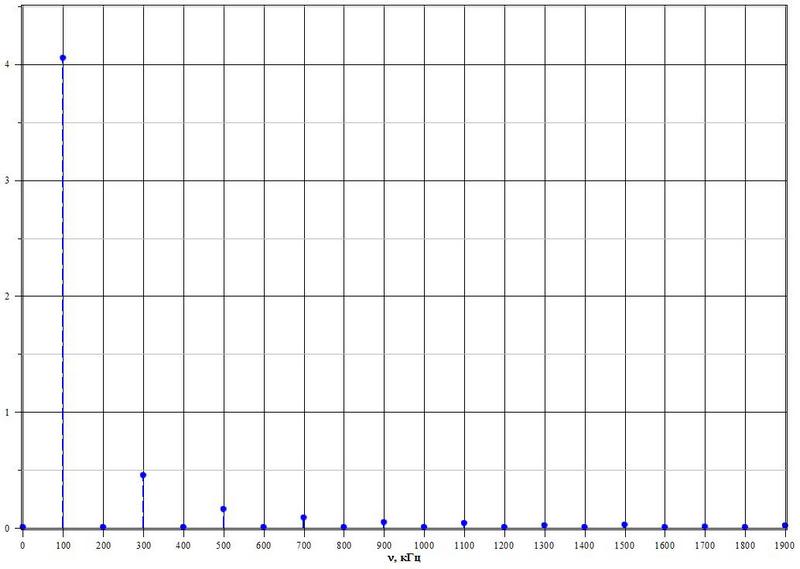
Как и в теории основной частотой является: $100$ кГц, ну, и дальнейшие по важности составляющие на чатоте $300$ кГц, $500$ кГц, и т.д.
Вопрос:
Правильно ли я понимаю, что мою треугольную функцию можно представить, как:
$$2\sum_{j=1}^{N} A_j \sin\left(2\pi\nu_gjt+\phi_j\right).
Где:
A_j — амплитуды, соответсвующие частотам: $100$ кГц, $300$ кГц, $500$ кГц, и т.д.
\phi_j — соответственно фазы, соответсвтующие частотам: $100$ кГц, $300$ кГц, $500$ кГц, и т.д.
P.S. ДПФ делаю в Maple 17 стандартной командой FourierTransform(triangle, normalization=none).

[profrotter]

Babeuf в сообщении #738034 писал(а):

Правильно ли я понимаю, что мою треугольную функцию можно представить, как:

Можно, если ваша треугольная функция периодическая. Только вот ДПФ тут непричём, поскольку оно связано с отсчётами спектра дискретного сигнала, а ваша треугольная функция - непрерывна.

[HataD86]

зачем так сложно задавать функцию изначально?
используйте единичную функцию 1(t).