Требуется найти спектр оператора

в
![$L_{2}[-\pi;\pi]$ $L_{2}[-\pi;\pi]$](https://dxdy-01.korotkov.co.uk/f/4/b/c/4bccc90b3ef79d30686c07c91111d5f582.png)
.
Соображения примерно следующие: так как оператор компактен, то спектр

состоит из точечного спектра

и нуля. Точечный спектр найдем из уравнения

, а вопрос, собственно, в том, куда включить ноль.
В похожих задачах иногда удается подобрать

так, чтобы она обнуляла

. (В данном случае, просто

.) Тогда ядро было бы непусто, а соответственно, 0 принадлежал бы точечному спектру. Попробовал взять

, получилось

. Это, конечно, еще не о чем не говорит, но я подозреваю, что
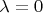
лежит не в точечном спектре, скорее всего в непрерывном. Как это показать?