1. Существует ли пример, не использующий факториал?
Если Вы знаете про радиус сходимости, то должны знать и то, что это понятие основывается на сравнении с геометрической прогрессией. Отсюда и вывод: чтобы радиус был нулём/бесконечностью, надо, чтобы коэффициенты убывали/росли быстрее любой геометрической прогрессии. Можете ли Вы сочинить что-нибудь, растущее быстрее
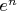
, не используя факториала?...
Здесь же степень константа (в каждом слагаемом), так что ничто не мешает считать, что

. Просто ради удобства записи.
Дело не в том, что она константа, а в том, что она целая. И считают по определению вовсе не

, а

.