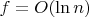
означает, что

Не совсем (если квантор поставить ещё), кстати. Вот описание
_hum_ полное.
А что означает

?
Оно могло бы означать

. Но лучше бы они так тогда и писали. Равенство в записях

— не то же самое, что обычное

— это просто синтаксис, потому лично я не вижу ничего хорошего в путании записями вида

.
-- Пн апр 15, 2013 02:05:55 --Где-то видел обозначения вида

— вот тут уже и

обозначает один конкретный объект — множество соответствующих функций.