Пытаюсь разобраться с критерием Саркади (в варианте Большева&Смирнова).
Если я правильно понимаю, то в выборке

назначается некоторый

-ый элемент. Оценка среднего
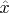
делается так, что все элементы выборки берутся с единичным весом,

-ый элемент берется с весом

. По идее такая оценка все равно остается несмещенной и подчиняется нормальному распределению с центром в истинном центре распределения, из которого взята выборка, и дисперсией

. Далее удаляем из выборки

-ый элемент, а из оставшихся вычитаем оценку центра. По Большеву&Смирнову новая случайная величина

опять же подчиняется нормальному распределению с центром 0 и стандартом

. Вот тут не совсем понятно, почему дисперсия не

? Ведь это разность двух случайных величин с одинаковым центром и дисперсиями

и

. Или между ними есть отрицательная корреляция?
Далее для каждого

-го элемента выборки

делается оценка дисперсии

, которая (умноженная на

) подчиняется распределению Пирсона с

степенями свободы. Вот тут не понятно два момента. Первое, почему не теряется степень свободы в распределении Пирсона - сколько слагаемых, столько и степеней свободы? Ведь оценка центра проводилась по той же выборке. Или за счет того, что не совсем по той же выборке, все слагаемые остаются независимыми? Второе - почему при оценке дисперсии используются не все оставшиеся элементы выборки, а только те, порядковый номер которых больше, чем

? Зачем терять степени свободы? К тому же на выходе тогда получается величина, подчиняющаяся разным распределениям, а если использовать все оставшиеся элементы, то распределение у всех дисперсий одно и то же. Зачем тогда усложнять? К тому-же возникает опасность, что выборка упорядочена, и тогда оценки дисперсий окажутся сильно заниженными. Не логичнее ли в качестве оценки дисперсии

-го элемента использовать
