геометрия (ГИА)

[ewert]

Ну хорошо. Если говорить о напрашивающихся чисто геометрических соображениях, то они дают вот что (ТС это уже отмечал с самого начала). Если задачка корректна, то площадь $S$ должна зависеть только от радиуса $R$, но не от наклона правой стороны $DC$. Тогда это же верно и для площади левого треугольничка $ABM$, т.е. 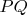точка пересечения диагоналей $M$, независимо от наклона правой касательной, должна находиться на вертикальном отрезке $PQ$, где $P$ и $Q$ -- это верхняя и нижняя точки касания. Или, что эквивалентно: если точка пересечения диагоналей лежит на этом вертикальном отрезке, то правая сторона $DC$ действительно касается окружности.

Эти соображения действительно достаточно очевидны и достаточно напрашиваются. Раздражает то, что для последнего утверждения, носящего чисто геометрический характер, как-то не просматривается столь же геометрического по характеру доказательства; в любом случае требуется какая-то возня с формулами.

Самый элементарный и требующий минимума изобретательности способ из тех, что мне приходили в голову, выглядит так. Пусть $x=|DP|$ и $y=|CQ|$ -- расстояния от правых вершин до соответствующих точек касания. Нетрудно заметить: если правая сторона касается окружности, то треугольник $DOC$, где $O$ -- центр окружности, -- прямоугольный и, следовательно, $xy=R^2$. Ясно также, что последнее равенство является критерием касательности, т.е. что доказать достаточно следующее утверждение: если $M\in PQ$, то $xy=R^2$.

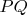
Первое, что напрашивается -- воспользоваться подобием треугольников $DMP$ и $DBA$ с одной стороны и треугольников $CMQ$ и $CAB$ с другой. Положение точки $M$ на вертикальном отрезке $PQ$ определяется, например, расстоянием $h=MQ$; остаётся лишь выразить $x$ и $y$ через $h$, после чего перемножить. Это уже дело техники:

$\dfrac{h}{2R}=\dfrac{y}{R+y} \quad \Rightarrow \quad y=\dfrac{Rh}{2R-h};$

$\dfrac{2R-h}{2R}=\dfrac{x}{R+x} \quad \Rightarrow \quad x=\dfrac{R(2R-h)}{h};$

$x\cdot y=R^2.$

Всё равно какое-то занудство. Непонятно, по каким принципиальным причинам всё так удачно сокращается.

[matidiot]

ewert в сообщении #681440 писал(а):

Раздражает то, что для последнего утверждения, носящего чисто геометрический характер, как-то не просматривается столь же геометрического по характеру доказательства; в любом случае требуется какая-то возня с формулами.
..................................................................................................................................................................
Всё равно какое-то занудство. Непонятно, по каким принципиальным причинам всё так удачно сокращается.

Просто Вы привыкли к геометрическим задачам линейного типа, которые решаются сразу без составления уравнения или с помощью простых отношений с использованием подобия, а эта задача оказалась существенно нелинейной (использовалась теорема Пифагора, см. выше у Total). Но, когда решаем текстовую задачу на "движение", которая сводится к полному квадратному уравнению (без уравнений такие задачи практически не решаются арифметическим способом), мы не печалимся по этому поводу.

[b45]

Решается достаточно просто....
Квадрат является частным случаем трапеции...
А для него найти радиус вписанной окружности зная его площадь ничего не стоит.
В этой задаче R= квадратному корню из S

[Shadow]

(Оффтоп)

b45 в сообщении #707194 писал(а):

Решается достаточно просто....

Любая сложная задача имеет простое, легкое для понимания неправильное решение