Вообще у меня вот такая ситуация : я решал УрЧП (задача Неймана в кольце для уравнения Лапласа). Решение представилось в виде ряда. Потом по заданию мне нужно свернуть этот ряд. Полностью это выглядит так :
![$$
u(r,\varphi) = w_0 + \frac {1} {\pi} \int\limits_{0}^{2 \pi} [\theta(\psi) \sum\limits_{n=1}^{\infty} \frac{(r^n+\frac{1} {r^n}) R^{n+1} \cos(n (\psi - \varphi))} {n (R^{2n} - 1)} - \gamma(\psi) \sum\limits_{n=1}^{\infty} \frac{(r^n+\frac{R^{2n}} {r^n}) \cos(n (\psi - \varphi))} {n (R^{2n} - 1)} ] d\psi
$$ $$
u(r,\varphi) = w_0 + \frac {1} {\pi} \int\limits_{0}^{2 \pi} [\theta(\psi) \sum\limits_{n=1}^{\infty} \frac{(r^n+\frac{1} {r^n}) R^{n+1} \cos(n (\psi - \varphi))} {n (R^{2n} - 1)} - \gamma(\psi) \sum\limits_{n=1}^{\infty} \frac{(r^n+\frac{R^{2n}} {r^n}) \cos(n (\psi - \varphi))} {n (R^{2n} - 1)} ] d\psi
$$](https://dxdy-03.korotkov.co.uk/f/6/4/b/64b83cab7572a5be41796487044a25b482.png)
, где на
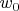
можно не обращать внимание,

и

- функции из краевых условий. Так вот, мне нужно свернуть все какие есть ряды, а потом уже, имея конкретные

и

, предъявить решение. Просто если я не сверну, то ответ будет в виде ряда. Этого бы не хотелось.