Термоядерная реакция

[VanyaZZ]

Увидел я недавно на хабре http://habrahabr.ru/post/167523/ такой список термоядерных реакций:
1) 2D+3T -> 4He (3.5 MeV) + n (14.1 MeV)
2) 2D+2D -> 3T (1.01 MeV) + p (3.02 MeV) 50%
2D+2D -> 3He (0.82 MeV) + n (2.45 MeV) 50%
3) 2D+3He -> 4He (3.6 MeV) + p (14.7 MeV)
4) p+11B -> 34He + 8.7 MeV
и у меня возник вопрос. Если в первой реакции полученная энергия выделяется с гелием и нейтроном, во второй - с тритием и протоном, в третей - с гелием и нейтроном, то какая частица переносит полученную энергию в четвертой реакции ?

[BISHA]

VanyaZZ в сообщении #682181 писал(а):

то какая частица переносит полученную энергию в четвертой реакции ?

Обычно это гамма лучи.

[Munin]

Четвёртая реакция пишется так:
$p+{}^{11}\mathrm{B} \to 3{}^{4}\mathrm{He}+8.7\text{ MeV}$
Теперь видно, что в результате реакции получаются три частицы.

Из кинематики известно, что если частиц две, то законы сохранения энергии и импульса однозначно задают энергию каждой частицы в системе центра масс (с. ц. м.). А вот если частиц три, то возникает неопределённость в задаче. Фактически, частицы вылетают каждый раз с разными энергиями каждая. Поэтому, в отличие от реакций 1-3, однозначно указать энергии каждой из трёх $\alpha$-частиц нельзя. Можно указать только суммарный энергетический эффект реакции. Он будет как-то случайно распределён между этими тремя частицами.

BISHA в сообщении #682232 писал(а):

Обычно это гамма лучи.

Я вам уже триста раз говорил не высказываться на темы, в которых вы ничего не смыслите.

[VanyaZZ]

Munin в сообщении #682268 писал(а):

Четвёртая реакция пишется так:
$p+{}^{11}\mathrm{B} \to 3{}^{4}\mathrm{He}+8.7\text{ MeV}$
Теперь видно, что в результате реакции получаются три частицы.

Из кинематики известно, что если частиц две, то законы сохранения энергии и импульса однозначно задают энергию каждой частицы в системе центра масс (с. ц. м.). А вот если частиц три, то возникает неопределённость в задаче. Фактически, частицы вылетают каждый раз с разными энергиями каждая. Поэтому, в отличие от реакций 1-3, однозначно указать энергии каждой из трёх $\alpha$-частиц нельзя. Можно указать только суммарный энергетический эффект реакции. Он будет как-то случайно распределён между этими тремя частицами.

BISHA в сообщении #682232 писал(а):

Обычно это гамма лучи.

Я вам уже триста раз говорил не высказываться на темы, в которых вы ничего не смыслите.

Спасибо.

[Munin]

Пожалуйста!

(Оффтоп)

(Доброе слово и кошке приятно.)

[druggist]

Munin в сообщении #682268 писал(а):

Фактически, частицы вылетают каждый раз с разными энергиями каждая

А вероятность вылететь с данной энергией можно рассчмтать? Какая будет зависимость от энергии?

[Munin]

druggist в сообщении #682407 писал(а):

А вероятность вылететь с данной энергией можно рассчмтать?

Можно. Но это гораздо более сложная штука :-) Называется эта область "кинематика элементарных частиц", и по ней толстые учебники написаны. (В школьной физике кинематика - это то, что касается движения и ускорений, то есть векторов в обычном пространстве; а в ФЭЧ это ещё и элементарные геометрические расчёты в пространстве векторов энергии-импульса.) В качестве введения:
Хелзен, Мартин. Кварки и лептоны.
Копылов. Всего лишь кинематика. (Библиотечка Квант)
Серьёзная:
Бюклинг, Каянти. Кинематика элементарных частиц.

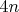
Общий принцип такой: в пространстве 4-мерных параметров вылетающих частиц, за счёт ограничений на суммарные энергии и импульсы, выбирается некоторое подмногообразие (учтите, что пространство - $4n$-мерное, где $n$ - число частиц). И это многообразие считается "заполненным" вероятностью равномерно.

Пример: пусть частица $m_0$ распадается на две частицы $m_1$ и $m_2,$ причём выполняется $m_0>m_1+m_2.$ Тогда в с. ц. м. исходный 4-вектор энергии-импульса имеет вид $(m_0,\mathbf{0})$ (вертикальный), и он раскладывается в сумму векторов $(m_1\gamma_1,m_1\mathbf{v}_1\gamma_1)$ и $(m_2\gamma_2,m_2\mathbf{v}_2\gamma_2),$ каждый из которых лежит на верхней полости двухполостного гиперболоида (на массовой поверхности). Откладывая вниз от конца исходного вектора второе слагаемое с обратным знаком, получаем нижнюю полость гиперболоида. Две полости - верхняя для первого слагаемого, нижняя для второго слагаемого - пересекаются по окружности (существование пересечения обеспечено выбранным условием на массы $m_0>m_1+m_2$). Точки этой окружности - возможные решения, они удовлетворяют сохранению и энергии, и импульса, поскольку удовлетворяют правилу суммы векторов. Теперь мы должны считать все эти точки равновероятными. Это нам даст равные вероятности вылетания частиц по любому направлению - одна в одну сторону, другая в противоположную. Тривиальный результат в с. ц. м., но теперь мы можем перевести его в другую систему отсчёта, и найти угловые распределения вероятностей. (Здесь надо вспомнить, что пространство 4-мерное, и реально речь идёт не об окружности, а о сфере.) Кроме того, на самом деле равновероятность всех точек может быть нарушена за счёт каких-то законов взаимодействия частиц - например, спинов - это уже называется динамикой, как и вообще вероятность такого процесса распада.

Для трёх частиц теория занимает где-то пол-учебника :-)

[druggist]

Munin в сообщении #682567 писал(а):

Кроме того, на самом деле равновероятность всех точек может быть нарушена за счёт каких-то законов взаимодействия частиц - например, спинов - это уже называется динамикой, как и вообще вероятность такого процесса распада.

И все же, без учета взаимодействия, массы трех частиц равны(одинаковые частицы), ...какой будет вероятность частице иметь энергию $p(E)$? Напрашивается равномерное распределение от 0 до $E_\max$...

[BISHA]

Munin в сообщении #682268 писал(а):

Я вам уже триста раз говорил не высказываться на темы

Гамма излучение, в большинстве случаев, возникает при ядерных реакциях.
Да, мой ответ неточен, толком не посмотрел на приведенный пример.

[Munin]

druggist в сообщении #682573 писал(а):

И все же, без учета взаимодействия, массы трех частиц равны(одинаковые частицы), ...какой будет вероятность частице иметь энергию $p(E)$? Напрашивается равномерное распределение от 0 до $E_\max$...

Нет, не равномерное. Если частица около конца возможного диапазона, возможности для других частиц уменьшаются - говорят "уменьшается фазовое пространство", хотя оно строго говоря не фазовое пространство из классической гамильтоновой механики. А если частица вблизи середины диапазона, возможности для других частиц увеличиваются. Считается, что все точки "фазового пространства" равновероятны. Таким образом, вероятность имеет вид какой-то гладкой кривой от нуля до горба и снова до нуля. Вот формулы точной я не помню, и тут не выведу. Но уже в Хелзене-Мартине это есть.

Например, на этой кривой был основан поиск массы нейтрино при $\beta$-распаде (сейчас известно, что для него не хватает точности, но как пример эксперимента он много где описан). Если нейтрино безмассовое, то кривая подходит к краю диапазона одним образом, а если масса мала, но конечна - другим образом.

-- 11.02.2013 23:19:35 --

BISHA в сообщении #682587 писал(а):

Гамма излучение, в большинстве случаев, возникает при ядерных реакциях.

Да, верно, но это не имеет ни малейшего отношения к вопросу.

BISHA в сообщении #682587 писал(а):

Да, мой ответ неточен

Нет, он просто ни к селу ни к городу.

[druggist]

Munin в сообщении #682655 писал(а):

Нет, не равномерное. Если частица около конца возможного диапазона, возможности для других частиц уменьшаются - говорят "уменьшается фазовое пространство", хотя оно строго говоря не фазовое пространство из классической гамильтоновой механики. А если частица вблизи середины диапазона, возможности для других частиц увеличиваются.

Так эти "возможности" еще больше увеличиваются, если частица в начале диапазона(т.е., имеет нулевую энергию). Суммарная энергия задана, радиус-вектор состояния системы бегает по гиперсфере в фазовом пространстве системы (если исключить пространственные координаты это будет 9-мерное пространство). Есть еще закон сохранения импульса, но он принципиально не изменит ситуацию, для одинаковых частиц $p(E)$ будет монотонно спадающее, без горба

[Munin]

Да, вот и я запутался. Диапазон несимметричный, вы правы. Надо за правильными формулами в учебники лезть, или считать (достаточно много для моей лени сегодня вечером).

druggist в сообщении #682699 писал(а):

Есть еще закон сохранения импульса, но он принципиально не изменит ситуацию

Он уже учтён, ведь наши векторы - это векторы энергии-импульса.

Думаю, вы сможете сами найти правильную формулу вероятности, или посмотреть в указанной литературе... если вам интересно, то вам полезно будет сделать это своими руками.