Добрый день!
Помогите, пожалуйста, прояснить вопрос.
Не вызывает сомнений, что ряд

сходится. Во-первых, общий член ряда на бесконечности эквивалентен

, во-вторых для всех

выполняется

, а

. То есть, как ни крути.
Однако Mathematica и Wolfram Alpha со мной не соглашаются.
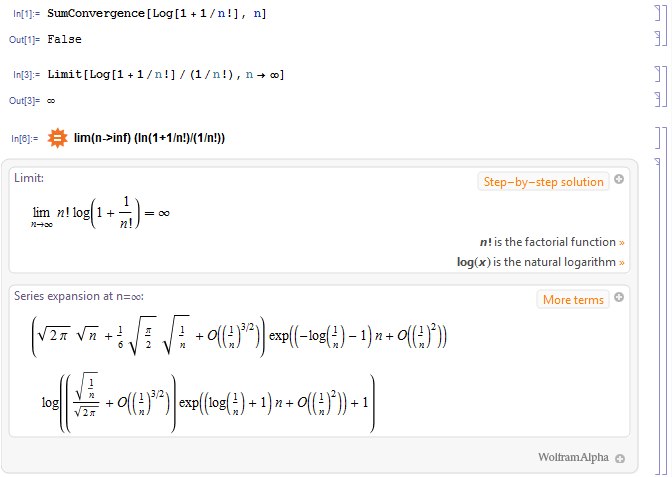
У них и ряд расходится, и эквивалентности нет.
Подозреваю, что под факториалом программа понимает функцию вещественного аргумента. И тем не менее, не понимаю, в чём тут подвох.
Господа математики, объясните, пожалуйста.