Здравствуйте. Я инженер в нефтедобывающей компании. Каюсь, не могу решить интеграл

С1 - константа
Есть готовый
ответ в учебнике, но я хочу проверить его
![$\int\limits_0^T {\left( {{C_1} - p(t)} \right){t^2}dt} = {C_1} \cdot \frac{{{T^3}}}{3} - \left[ {\sum\limits_{i = 1}^N {p({t_i}){t_i}^2} + \frac{1}{2}p(T){T^2}} \right] \cdot \Delta t$ $\int\limits_0^T {\left( {{C_1} - p(t)} \right){t^2}dt} = {C_1} \cdot \frac{{{T^3}}}{3} - \left[ {\sum\limits_{i = 1}^N {p({t_i}){t_i}^2} + \frac{1}{2}p(T){T^2}} \right] \cdot \Delta t$](https://dxdy-04.korotkov.co.uk/f/7/9/5/7959a16638b455a14659db592d02110382.png) Условие:
Условие:в скважине замеряется рост давления p(t) через равные промежутки времени

T – полное время замера, N – номер предпоследнего замера, т.е.

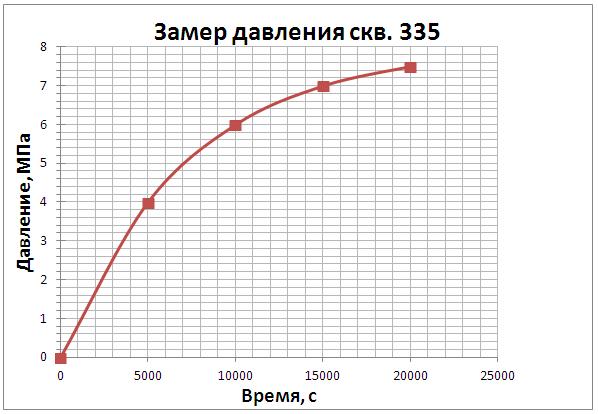
Рис. 1 Дискретный замер давления p(t)
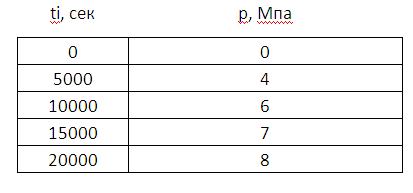
Табл. 1 Дискретный замер давления p(t)
Мое недо-Решение.Я тут было начал решение, но застопорился

Далее интегрирование по частям



Вот тут-то на последнем интеграле я и застопорился, потому что чушь получается

Проблема в том, что p(t) не функция, а дискретный точный замер