Разобраться в суммах n-х степеней

[loginsin]

Deggial: Отделено от темы Открытые проблемы форумчан как несодержащее объективную проблему и содержащее неявные вопросы.

Поведую, как я когда-то находил суммы степени n натурального ряда.
$S=\Sigma i^n$
Способ довольно примитивный, но громоздкий с возрастанием n. Спросите, почему для меня это открытый вопрос? Очень просто: мне так и осталась непонятной закономерность, на основе которой этот алгоритм. Нашлась она эмпирическим способом, но понять откуда ноги растут - не удалось (да и было это давно).
Суть в следующем: для любого $n$, находя разности соседних членов каждой из последующей последовательностей (т.е. разность соседних членов $i$-ой последовательности образует новую $(i+1)$-ую), мы получим $n$-ую последовательность, состоящую из $n!$.

Поясню на примере $n=5$:
$a_0 : 1^5, 2^5, 3^5, 4^5, 5^5, 6^5, 7^5, 8^5, 9^5, 10^5$
тот же ряд в числах
$a_0 : 1, 32, 243, 1024, 3125, 7776, 16807, 32768, 59049, 100000$
$a_1 : 1, 31, 211, 781, 2101, 4651, 9031, 15961, 26281, 40951
$a_2 : ?, 30, 180, 570, 1320, 2550, 4380, 6930, 10320, 14670$
$a_3 : ?, 30, 150, 390, 750, 1230, 1830, 2550, 3390, 4350$
$a_4 : ?, ?, 120, 240, 360, 480, 600, 720, 840, 960$
$a_5 : ?, 120, 120, 120, 120, 120, 120, 120, 120, 120 \equiv 5!$

Для бОльшей наглядности я позволил себе некоторые упрощения с единицей в начале, иначе первые несколько членов в последней последовательности будут отклоняться в ту или иную сторону от $5!$.
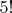
Соответственно, сумму $S=\Sigma i^n$ я находил в обратном порядке, нахождением суммы каждой последующей последовательности вверх, получая искомое. Но связи между рядом $i^n$ и рядом $a_n = n! я не нашел (точнее не разбирался в том, почему эта связь вообще существует).
Кстати, исходя из этой закономерности, для данного частного случая с $n=5$, ряд $i^5$ будет всегда иметь числа, последней цифрой которых будет последняя цифра числа $i$ (т.е. ($i^5 \mod 10) = (i \mod 10)$).
В дополнение: для $n=6$ будет ($i^6 \mod 10) = ((2(i \mod 10)+1) \mod 10)$

Возможно, я объяснил несколько косоязычно, но буду рад внести поправки, если возникнут вопросы.

[nnosipov]

loginsin в сообщении #678846 писал(а):

мне так и осталась непонятной закономерность, на основе которой этот алгоритм.

Почитайте где-нибудь про многочлены Бернулли.