Если взять (упрощенно, но мне это подходит), что абсцисса первой точки
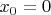
тогда через абсциссу второй точки длина дуги равна:

Возможно ли из этого выразить коэффициент a ???
-- 30.01.2013, 15:02 --Всем спасибо, вопрос закрыт. Помогли на соседнем форуме:

Это приближенная формула, которой для решения моей конкретной задачи вполне достаточно. Точного решения нет.