При каких х последовательность ограниченна

[azmt]

Здравствуйте. При каких $x$ последовательность $\{1+x+x^2+...+x^n\}$ будет ограниченной. Очевидно, что подходит $x=-1$. Принимается ли такой ответ в качестве решения? Если нет, помогите, пожалуйста, разобраться. Других решений найти не удалось.

[SpBTimes]

сверните сумму геометрической прогрессии

[azmt]

$1+x+x^2+...+x^n=\frac{1(x^n-1)}{x-1}$, при этом $x $\not= 1$. Докажем,например, что $-1<\frac{1(x^n-1)}{x-1}<1$.
$x^n-1<x-1$; $x^n<x$.
$x^n-1>-x+1$; $x^n>2-x$;
$x>\sqrt[n]{2-x}$;
Из неравенства следует, что значения $x$ должны лежать на отрезке $0<x<1$, при этом $x \not= 0$.

[Slow]

Вообще говоря $-1 \leq x<1$

[Someone]

azmt в сообщении #672244 писал(а):

$x^n-1<x-1$; $x^n<x$.

Неверно.

azmt в сообщении #672244 писал(а):

$x^n-1>-x+1$; $x^n>2-x$;

Неверно.

azmt в сообщении #672244 писал(а):

Из неравенства следует, что значения $x$ должны лежать на отрезке $0<x<1$, при этом $x \not= 0$.

Неверно. Почему вдруг $x$ должен быть положительным?

Кроме того, сам подход неверный. Вы пишете: «Докажем,например, что $-1<\frac{1(x^n-1)}{x-1}<1$.» И вместо того, чтобы доказывать это неравенство, пытаетесь его решить (неправильно). А если вместо этого неравенства взять $-10<\frac{1(x^n-1)}{x-1}<10$? А почему не $-1000<\frac{1(x^n-1)}{x-1}<1000$?

[azmt]

Я так понимаю, что можно взять и неравенство $-1000<\frac{1(x^n-1)}{x-1}<1000$. Только при этом значения $x$ должны быть другими.
Т.е. $\frac{1(x^n-1)}{x-1}<1000$ ; $x^n-1<1000(x-1)$
$x^n<1000x-1000+1$; $x^n<1000x-999$
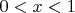
Таким образом $\frac{1(x^n-1)}{x-1}<1000$ - справедливо, если $x$ принимает значения $x<\sqrt[n]{1000x-999}$. В чём моя ошибка? Просто я думал, что для целей задачи достаточно показать при каких $x$ последовательность будет ограниченна на произвольном интервале, я взял $-1...1$. В условии же не сказано на каком именно интервале. По поводу "$x$ должны лежать на отрезке $0<x<1$" - видимо эту фразу не надо было писать, она здесь лишняя.

[azmt]

Любой член данной геометрической прогрессии может быть вычислен по формуле: $a_n=1x^{n-1}$. Тогда по определению для ограниченной последовательности: $x^{n-1}<1$, откуда следует $\sqrt[n-1]{x^{n-1}}<\sqrt[n-1]1$. Таким образом $x$ должен принимать значения $x<1$.

[Slow]

В чем проблема вообще? Видно же что если свернуть последовательность через сумму геометрической прогрессии, то только при $-1 \leq x <1$ она будет конечна.

[azmt]

Если подставить $x=0$ в формулу $\frac{1(x^n-1)}{x-1}$,
то имеем $\frac{1(0^n-1)}{0-1}$, то есть последовательность чисел $1,1,1,1...$. Нам же нужно доказать, что каждый член последовательности $|a_n|<M (M>0)$, я выбрал $M=1$. Где я ошибся?

[SpBTimes]

azmt в сообщении #672649 писал(а):

то есть последовательность чисел $1,1,1,1...$

Глупости, это же сумма уже равна 1

[azmt]

Благодарю за ответы.
SpBTimes, мы же и рассматриваем последовательность сумм геометрической прогрессии, судя по условию. В последовательности $1,1,1,..$ каждое число представляет сумму при $x=0$. Разве не так?

[INGELRII]

А что, запрещено тупо воспользоваться теоремой Коши-Адамара? Задача же, черт возьми, про ряды и их сходимость. Значит, можно пользоваться всеми теоремами, связанными с рядами.

[azmt]

Ну просто задача из самого начала учебника по анализу. Ряды там только где-то к середине, их знание видимо не предполагается. Может для решения задачи достаточно привести примеры значений, например $x=-1, x=0$, при которых она ограничена. То есть не требуется приводить аналитического решения.

[SpBTimes]

azmt в сообщении #672657 писал(а):

В последовательности $1,1,1,..$ каждое число представляет сумму при $x=0$. Разве не так?

Не так. Это сумма вашей прогрессии, если $x = 0$