Критерий Эйзенштейна

[nnosipov]

Будем называть многочлен с целыми коэффициентами удачным, если он удовлетворяет критерию Эйзенштейна. Очевидно, многочлен $f(x)=x^q-x-1$, где $q$ --- нечётное простое число, удачным не является. Можно ли сделать так, чтобы "сдвинутый" многочлен $g(x)=f(ax+b)$ стал удачным?

[nnosipov]

Под "удовлетворяет критерию Эйзенштейна" имелось в виду, конечно, следующее: существует такое простое число $p$, что старший коэффициент многочлена на $p$ не делится, все остальные коэффициенты делятся на $p$, а свободный коэффициент не делится на $p^2$.

[Cash]

Что-то слишком все просто получается.
Пусть $p$ - подходящее под критерий Эйзенштейна простое число для $g(x)$
Тогда, рассматривая старший и свободный члены, видим что $(a,p)=1$, $(b,p)=1$
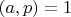
Рассматривая коэффициент при $x^{q-1}$
$qa^{q-1}b \equiv 0 \pmod p$, откуда $p=q$
Смотрим на коэффициент при $x$
$qb^{q-1}a-a \equiv 0 \pmod q$
$a \equiv 0 \pmod q$, что противоречит $(a,q)=1$

Где ошибка?

-- Пн янв 14, 2013 11:36:16 --

Нужно доказывать рациональность $a$ и $b$?

[nnosipov]

Cash в сообщении #671415 писал(а):

Что-то слишком все просто получается.

Спасибо, что это заметили. Просто я проморгал очевидное противоречие, пардон. В общем, не задача оказалась.