Let

is a convex quadrilateral.

is the intersection point of the lines

and

.

is the intersection point of the lines

and


is the intersection point of the diagonals

and

. Through

is drawn a line intersecting the line

at the point

. Through the vertices

,

,

,

are drawn lines parallel to the line
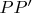
intersecting the line

at the points

,

,

,

, respectively. Prove that:
a)
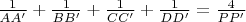
;
b)
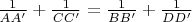
.