Так

по условию.
Ой! Прошу прощенья... Зачеркнул
Дело в том,что задача предлагалась для 10 класса..как бы поаккуратнее это объяснить на уровне 10 класса?
Боюсь, что придется это все также и объяснять, только неявно. (т.е. пусть для

это неверно. Берем последовательность рациональных

, которые сходятся к

, используем непрерывность и приходим к противоречию)
-- Чт янв 03, 2013 19:13:46 --2. Доказать,что для каждого натурального числа

,такого,что

,существует хотя бы одно натуральное число

, для которого число

является составным.
Нетрудно видеть, что

- нечетно,

- квадратичный невычет по модулям

при

(случай

следует рассмотреть отдельно), либо

либо

(т.е. надо вычеркнуть случаи

). Интересно, это сильно поможет?

upd: можно еще отсеивать числа, решая сравнения

для
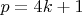
. В общем, мой метод прост: решето. Отсеять достаточно много, пока не останется 1-2 числа, а с ними уж отдельно разобраться. Больше я ничего не придумал
