Геометрическая задача про конус

[Kosmos-1729]

Подскажите пожалуйста, правильно ли решение и можно ли как-то упростить ответ.

Задачка:
"В конусе, радиус основания которого равен $R$, а образующая наклонена к плоскости основания под углом $\alpha$, через вершину проведена плоскость, которая образует с высотой конуса угол $\beta$. Найдите площадь поперечного сечения."



1. Мы можем предположить, что в задаче говориться о прямом круговом конусе. Поскольку дан радиус основания $R$ (следовательно в основании круг) и "образующая наклонена к плоскости основания с углом $\alpha$" (значит конус прямой).
2. Раз " через вершину проведена плоскость, которая образует с высотой конуса угол $\beta$", то это поперечное сечение представляет собой равнобедренный треугольник.

Дано: радиус основания $=$ $R$;
угол между образующей и плоскостью основания $=$ $\alpha$;
угол между высотой и попречным сечением $=$ $\beta$.
Найти: площадь поперечного сечения - $S$.
Решение:
1. Найдём высоту конуса $h = PO$ (рис. 1);
$PO = R \tg \alpha$;
2. Найдём образующую конуса $PA$ (рис. 3);
Треугольник $PAO$ - прямоугольный, и $PO = R \tg \alpha$, $AO = R$, угол $AOP = 90°$. По теореме Пифагора: $PA = \sqrt{R^2 + R^2 \tg^2 \alpha} = R \sqrt {1 + \tg^2 \alpha}$;
$PA = PB = PC$, поскольку все эти отрезки являются образующими конуса;
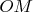
3. Найдём $OM$ (рис. 3);
$OM = R \tg \alpha \times \tg \beta$;
4. Найдём $MC$ (рис. 2);
$MC = \sqrt{R^2 - (R \tg \alpha \times \tg \beta)^2} = R \sqrt{1 - \tg^2 \alpha \times \tg^2 \beta}$;
$BC = 2 \times MC = 2 R \sqrt{1 - \tg^2 \alpha \times \tg^2 \beta}$;
5. Найдём $PM$ (рис. 1);
$PM = \sqrt{(PC)^2 - (MC)^2} = \sqrt{(R \sqrt{1 + \tg^2 \alpha})^2 - (R \sqrt{1 - \tg^2 \alpha \times \tg^2 \beta})^2} = R \sqrt{(1 + \tg^2 \alpha) - (1 - \tg^2 \alpha \times \tg^2 \beta)} = R \tg \alpha \sqrt{\tg^2 \beta + 1}$;
6. Найдём площадь поперечного сечения - $S$;
S $=$ площади равнобедренного треугольника $PBC$ (рис. 1).

Воспользуемся формулой $S_\Delta = 0,5 \times b \times h$;
Нам известно, что:
$a = PB = PC = R \sqrt {1 + \tg^2 \alpha}$;
$b = BC = 2 R \sqrt{1 - \tg^2 \alpha \times \tg^2 \beta}$;
$h = PM = R \tg \alpha \sqrt{\tg^2 \beta + 1}$;

$S = 0,5 \times 2 R \sqrt{1 - \tg^2 \alpha \times \tg^2 \beta} \times R \tg \alpha \sqrt{\tg^2 \beta + 1} = R^2 \times \tg \alpha \times \sqrt{1 - \tg^2 \alpha \times \tg^2 \beta} \times \sqrt{\tg^2 \beta + 1}$.
Ответ: площадь поперечного сечения равна $R^2 \times \tg \alpha \times \sqrt{1 - \tg^2 \alpha \times \tg^2 \beta} \times \sqrt{\tg^2 \beta + 1}$ (квадратных единиц).

[Keter]

Вместо $a \times b$ пишите $a \cdot b$. То есть вместо \times -- \cdot

[Kosmos-1729]

Ага, благодарю Я её как раз не смог найти.

[alcoholist]

Kosmos-1729 в сообщении #664043 писал(а):

$PA = \sqrt{R^2 + R^2 \tg^2 \alpha} = R \sqrt {1 + \tg^2 \alpha}$

все-таки проще $R/\cos\alpha$

[Kosmos-1729]

alcoholist в сообщении #664259 писал(а):

все-таки проще $R/\cos\alpha$

Согласен, только я решил, если в одних местах решать через $\cos$, а в других через $\tg$, потом сложнее будет сокращать получившееся.

Да и строго говоря мне длина образующей ($a = R \sqrt {1 + \tg^2 \alpha}$) и не понадобилась для решения. Я в начале хотел найти площадь сечения конуса ($=$ равнобедренный треугольник) по формуле $S = \frac{b} {4} \cdot \sqrt {4a^2 - b^2}$, где $b$ - длина основание равнобедренного треугольника, а $a$ - длина одной из его равных сторон. Но потом подумал, что по формуле $S = b \cdot h$ решать будет проще.