пусть оператор умножения на независимую переменную

действует в
![$L_p[0,1], p \in [1,\infty]$ $L_p[0,1], p \in [1,\infty]$](https://dxdy-04.korotkov.co.uk/f/f/9/2/f92daf1aea3c02c9e6492be0729fe0cc82.png)
. Найти норму и ядро этого оператора. Выяснить, сюръективен ли оператор и совпадает ли его замыкание образа со всем пространством.
Вот мои идеи, сначала разобъем на два случай, первый

не бесконечность, тогда

, так как
![$t \in [0,1]$ $t \in [0,1]$](https://dxdy-01.korotkov.co.uk/f/0/1/d/01df98f22b2b1c9a0c617975dfbe543c82.png)
, то норма оператора в этом случае ограничена

, но не получается построить пример, доказывающий этот факт.
Во втором случае,
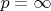
, имеем
![$||A x||=\inf_{\mu(A)=0} \sup_{[0,1]\A} |t x(t)|^p \le^{t \in [0,1] } ||x(t)||$ $||A x||=\inf_{\mu(A)=0} \sup_{[0,1]\A} |t x(t)|^p \le^{t \in [0,1] } ||x(t)||$](https://dxdy-01.korotkov.co.uk/f/4/2/f/42f664377711cb465c97bc03e0c765d782.png)
, то норма оператора в этом случае ограничена

, и опять не могу привести пример :( ну наверное они совпадут.
Ядро по идее состоит из

.
А сюръективность и про замыкание образа я не знаю, как проверить. Но ответ такой: оператор не сюръективен, причем замыкание образа совпадает со всем пространством только при

.
Помогите, пожалуйста, с решением задачи