Задача динамического программирования
Имеется

– начальное количество средств, которые нужно распределять в течение

лет между двумя отраслями I и II. Средства, вложенные в каждую отрасль, приносят за год определенный доход. Если вложить средства

в отрасль I, то за год получим доход

. Если вложить средства

в отрасль II, то за год получим доход

. При этом средства амортизируются (уменьшаются) так, что к концу года становятся равными для I отрасли

, а для II отрасли

.
По истечение года оставшиеся от

средства перераспределяются заново между отраслями I и II. Новых средств не поступает, доход в производство не вкладывается, а накапливается отдельно. Найти такой способ управления ресурсами (какие средства, в какие года и в какую отрасль вкладывать), при котором суммарный доход от обеих отраслей за

лет будет максимальным.
Решить задачу при следующих условиях:

,

,

,

,

,

.
Уравнение состояния



Целевая функция k-го шага


Целевая функция

Функциональные уравнения


III шаг

график этой функции при

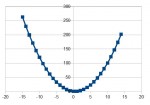
график этой функции при

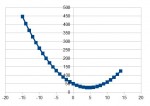
график этой функции при

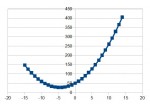
Как узнать когда у этой функции будет максимум?