A1
Пусть

--- вещественные числа в открытом
интервале

Докажите, что найдутся
различные индексы

, такие что

суть длины сторон остроугольного
треугольника.
A2
Пусть

--- коммутативная ассоциативная
бинарная операция на множестве
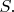
Предположим, что для любых элементов

и

в

найдется элемент

в

, такой что

(

может зависеть от

и

)
Докажите, что если

в

и

то

A3
Пусть
![$f:[-1,1]\to\mathbb{R}$ $f:[-1,1]\to\mathbb{R}$](https://dxdy-03.korotkov.co.uk/f/a/c/9/ac973c1b31706d7764c50e6ed516f87282.png)
--- непрерывная функция
такая что
(i)

для всех

из отрезка
![$[-1,1],$ $[-1,1],$](https://dxdy-01.korotkov.co.uk/f/c/3/e/c3e0de0d3ec1b0d0da69072bfd5926fc82.png)
(ii)

и
(iii) предел

существует и конечен.
Докажите, что такая функция

единственна и найдите

(в замкнутом виде).
A4
Пусть

и

--- целые числа,
причем

и пусть

и

---
интервалы на вещественной оси.
Пусть

---- множество чисел вида

, где

и

целые, причем

лежит в интервале

;

---
множество целых чисел

в интервале

таких что

лежит в

Докажите, что если произведение длин
интервалов

и

меньше чем

то

представляет
из себя пересечение

и некоторой
арифметической прогрессии.
A5
Пусть

--- поле остатков
по простому модулю


--- натуральное число.
Пусть

--- фиксированный вектор в


--- матрица

с элементами в

.
определим отображение

формулой

Пусть

обозначает

-ую композицию

с собой, т.е.

и

Определите все пары

, для которых существуют

и

такие что все

векторов


различны.
A6
Пусть

--- непрерывная вещественнозначная
функция на плоскости
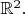
Предположим, что для любого прямоугольника

площади

интеграл

по

равен нулю.
Обязательно ли функция

--- тождественный нуль?
B1
Пусть

--- класс функций из

в

,
удовлетворяющий условиям:
(i) функции

и

лежат в

(ii) если функции

и

лежат в
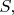
то функции

и

лежат в

(iii) если

и

лежат в

и

для всех

то функция

лежит в
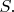
Докажите, что если функции

и

лежат в
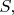
то функция

тоже лежит в
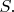
B2
Пусть

--- данный невырожденный
многогранник. Докажите, что найдется такая
константа

, что выполняется условие:
если объединение

шаров с суммой объемов

содержит поверхность многогранника

то

B3
Однокруговой волейбольный турнир

команд продолжается

день. Каждый день проходит

игр и
каждая команда играет ровно одну игру.
В итоге каждая сыграла с каждой ровно один
раз. Всегда ли можно выбирать каждый
день команду, победившую в этот день,
так, чтобы все

выбранных команд были различны?
B4
Предположим, что

и

для

Имеет ли последовательность

конечный предел при

(Здесь

обозначает натуральный логарифм

)
B5
Докажите, что для
любых двух ограниченных функций

существуют функции

такие что для всех

![$\[\sup_{s\in\mathbb{R}}\left(g_1(s)^xg_2(s)\right)=\max_{t\in\mathbb{R}}\left(xh_1(t)+h_2(t)\right).\]$ $\[\sup_{s\in\mathbb{R}}\left(g_1(s)^xg_2(s)\right)=\max_{t\in\mathbb{R}}\left(xh_1(t)+h_2(t)\right).\]$](https://dxdy-03.korotkov.co.uk/f/a/9/8/a981ebef9848c964cccaddc4140078ed82.png)
B6
Пусть

--- нечетное простое такое что

Определим перестановку

остатков по модулю

формулой

Докажите, что перестановка

четная если и только
если

Перевод на русский:
rus4.