Я попытался доказать следующим образом. Пусть диагональное представление матрицы
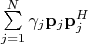
выглядит так
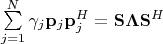
, где
![$\mathbf S = \left[\mathbf s_1 \mathbf s_2 ... \mathbf s_N\right]$ $\mathbf S = \left[\mathbf s_1 \mathbf s_2 ... \mathbf s_N\right]$](https://dxdy-02.korotkov.co.uk/f/9/0/2/902c1ade21c4a0188e6705cb6667042b82.png)
- унитарная матрица, а
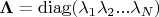
- диагональная матрица. Тогда для вектора

имеем
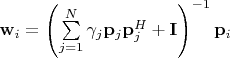
=
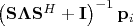
=
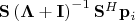
. Если ввести обозначение
![$\mathbf S^H\mathbf p_i = \mathbf \beta_i = \left[\beta_{i1}\beta_{i2}...\beta_{iN}\right]^T$ $\mathbf S^H\mathbf p_i = \mathbf \beta_i = \left[\beta_{i1}\beta_{i2}...\beta_{iN}\right]^T$](https://dxdy-04.korotkov.co.uk/f/b/8/3/b83625502aae5c9965563e9ee813b95b82.png)
, то вектор

можно записать как:
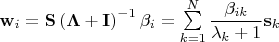
. Таким образом,
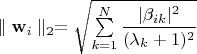
. Для матрицы
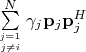
спарведливо следующее соотношение
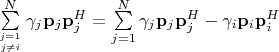
=
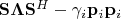
. Тогда по аналогии для вектора
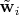
имеем
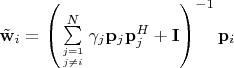
=
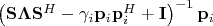
=
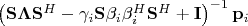
=
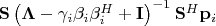
=
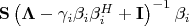
. Вот, собственно, и всё. На этом я запнулся, так как не знаю, что делать с матрицей
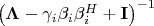
(как видно, она является недиагональной, и поэтому её не так просто обратить). Please HELP
