Шестой международный Киевский математический фестиваль
5-8.05.2007
Устная математическая олимпиада. 10 класс
5.05.2007, Киев, лицей №171 "Лидер"
Довывод
1. В клетчатом квадрате

отмечены центры всех
единичных квадратиков. Какое наименьшее число прямых, не параллельных
сторонам квадрата, нужно провести, чтобы вычеркнуть все отмеченные точки?
2. На бумаге в клеточку нарисован выпуклый многоугольник так, что
все его вершины находятся в вершинах клеток и ни одна из его сторон не идет
по вертикали или горизонтали. Докажите, что сумма длин вертикальных отрезков
линий сетки, заключенных внутри многоугольника, равна сумме длин
горизонтальных отрезков линий сетки внутри многоугольника.
3. Последовательность натуральных чисел

удовлетворяет условию

Докажите, что она содержит не
более одного точного квадрата.
4. Для положительных чисел

,

,

докажите неравенство:
![$$
\left( {1+\frac{x}{y}} \right)\left( {1+\frac{y}{z}} \right)\left(
{1+\frac{z}{x}} \right)\geqslant 2+\frac{2(x+y+z)}{\sqrt[3]{xyz}}.
$$ $$
\left( {1+\frac{x}{y}} \right)\left( {1+\frac{y}{z}} \right)\left(
{1+\frac{z}{x}} \right)\geqslant 2+\frac{2(x+y+z)}{\sqrt[3]{xyz}}.
$$](https://dxdy-04.korotkov.co.uk/f/7/9/0/7904c1c80d69a7f7c9351480af2c25d582.png)
5. Окружности

и

с центрами в точках

и

соответственно касаются внешним образом в точке

.
Окружность

с центром в точке

внутренним образом касается окружностей

и

в точках

и

соответственно. Общая касательная к
окружностям

и

в точке

образует хорду
окружности

с серединой в точке
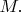
Докажите, что
 Вывод
Вывод
6. Найдите все функции

, удовлетворяющие условиям:
(1) если

, то

;
(2)

.
7.

--- доска размером

клеток. Назовем
диагональный ряд клеток положительной диагональю, если он параллелен

.
Какое наименьшее количество монет нужно разместить на клетках доски так,
чтобы каждая клетка доски либо сама содержала монету, либо находилась на
одной вертикали, горизонтали или положительной диагонали хотя бы с одной
клеткой, содержащей монету?
Письменная математическая олимпиада
6.05.2007, Киев, лицей №171 "Лидер"
апелляция - 7.05.2007, Конча Заспа, лагерь "Каштан"
8-й класс
1. Можно ли разрезать доску
размером

на изображенные фигурки, если нужно
использовать хотя бы по одной фигурке каждого
вида?

2. Найти все пары натуральных чисел

такие, что

3. Вершины 100-угольника покрашены
последовательно в белый и черный цвета. В одной из белых вершин
стоит фишка. Двое игроков по очереди выполняют две операции:
передвигают фишку в другую вершину по стороне 100-угольника и затем
вытирают какую-нибудь сторону. Игра заканчивается, когда нельзя
передвинуть фишку. Если в конце игры фишка стоит в белой вершине, то
выигрывает первый игрок, а если в черной, то второй. Имеет ли
кто-нибудь из игроков выигрышную стратегию? Если имеет, то кто?
4. На стороне

треугольника

отметили
точку

. Построить на сторонах

,

точки

,

соответственно
так, чтобы середины

и
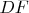
лежали на одной прямой с

, а
середины

и

лежали на одной прямой с

.
5. Есть набор камней весом

г.
Найти все

, при которых можно положить

и остальные

камней из набора соответственно на две чашки весов так, чтобы
получить равновесие.
9-й класс
1. Найти все пары натуральных чисел

такие, что

.
2. На стороне

треугольника

отметили
точку

. Построить на сторонах

,

точки

,

соответственно
так, чтобы середины

и
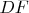
лежали на одной прямой с

, а
середины

и

лежали на одной прямой с

.
3. Есть набор камней весом

г.
Найти все

, при которых можно положить

и остальные

камней из набора соответственно на две чашки весов так, чтобы
получить равновесие.
4. Вершины 100-угольника покрашены
последовательно в белый и черный цвета. В одной из черных вершин
стоит фишка. Двое игроков по очереди выполняют две операции:
передвигают фишку в другую вершину по стороне 100-угольника и затем
вытирают какую-нибудь сторону. Игра заканчивается, когда нельзя
передвинуть фишку. Если в конце игры фишка стоит в белой вершине, то
выигрывает первый игрок, а если в черной, то второй. Имеет ли
кто-нибудь из игроков выигрышную стратегию? Если имеет, то кто?
5. Пусть

и

. Доказать, что
 10-й класс
10-й класс
1. Найти все пары натуральных чисел

такие, что

.
2. На стороне

треугольника

отметили
точку

. Построить на сторонах

,

точки

,

соответственно
так, чтобы середины

и
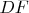
лежали на одной прямой с

, а
середины

и

лежали на одной прямой с

.
3. Есть набор камней весом

г.
Найти все

, при которых можно положить

и остальные

камней из набора соответственно на две чашки весов так, чтобы
получить равновесие.
4. Пусть

и

. Доказать, что


5. Вершины 100-угольника покрашены
последовательно в белый и черный цвета. В одной из вершин стоит
фишка. Двое игроков по очереди выполняют две операции: передвигают
фишку в другую вершину по стороне 100-угольника и затем вытирают
какую-нибудь сторону. Игра заканчивается, когда нельзя передвинуть
фишку. Если в конце игры фишка стоит в белой вершине, то выигрывает
первый игрок, а если в черной, то второй. Имеет ли кто-нибудь из
игроков выигрышную стратегию? Если имеет, то кто?