Что такое синглетное и триплетное состояния?

[Mitrandir]

Здравствуйте,
Собственно мой вопрос озвучен в заголовке. Что такое синглетное и триплетное состояния?
Неоднократно спрашивал у преподавателей и однокурсников, но ни определения, ни понимания того что же это не составил.
А в литературе этот вопрос игнорируется, прямо заговор какой то.

[fizeg]

Имеется в виду как это состояние преобразуется относительно какой-то группы (или, как это называют, к пространству какого представления группы относится это состояние), судя по всему вы имеете в виду цветную $SU(3)$

Я думаю будет легче, если сравнить это с группой вращений. Если ваш объект преобразуется относительно вращений тривиальным образом (т.е. никак, является скаляром), вы его можете описать одним числом. Синглетное (т.е. однокомпонентное) состояние тоже никак не чувствует преобразований из $SU(3)$, только в данном случае это комплексное число. Если речь о цвете, то синглетные состояния описывают бесцветные объекты.

Если же вращения как-то объект меняют, вы можете представить его в виде некоторого набора чисел-компонент, которые вращения перемешивают. Например вектор для трехмерных вращений можно представить как три числа. Для группы $SU(3)$ простейший пример - тоже трехкомпонентное, т.е. триплетное состояние, только опять же компоненты комплексные. Эти три компоненты отвечают компонентам для 3х разных цветов, пример очевиден: кварки 3х цветов.

-- 15.10.2012, 09:57 --

Хотя подумав еще раз, с большой вероятностью (а может даже и наверняка) имеется в виду приближенная симметрия $(u,d,s)$ применительно к легким адронам.

[Утундрий]

http://ru.wikipedia.org/wiki/%D0%9C%D1% ... 1%82%D1%8C, например.

[fizeg]

(Оффтоп)

Вот тебе и последствия сплошной ктп после третьего курса

[Munin]

Да, $SU(3)$ тут ни при чём: её синглет и триплет не могут сосуществовать в одной физической системе.

В литературе этот вопрос изложен там, где рассматриваются тождественные частицы и составленные из них состояния. Например, в ЛЛ-3 § 63. Но там общая теория. А здесь её узкий частный случай.

Цитата из меня с другого форума:

Цитата:

Пусть у нас два спина 1/2. Например, два электрона в coседних ячейках металла или в атоме гелия. Каждый из них имеет coстояния "вверх" и "вниз", так что всего получаются четыре комбинации (электроны пронумерованы, то eсть тождественностью не заморачиваемся, её потом добавляют): $|\uparrow\uparrow\rangle$, $|\uparrow\downarrow\rangle$, $|\downarrow\uparrow\rangle$, $|\downarrow\downarrow\rangle$. Полное представление получившихся четырёх coстояний получается из элементарных представлений как $2\otimes 2$ (в упрощённых обозначениях Хелзена-Мартина, полных не знаю, к сожалению).

Далеe, мы можем забыть про то, как эти электроны ориентированы по отдельности, и каким-то образом измерить их суммарную проекцию спина. Она может принимать значения +1, 0, -1 (это видно из того, что такие значения coответствуют явно перечисленным coстояниям). Ho что будет, eсли мы повернём двухэлектронную систему в пространстве как целое, или сами начнём поворачиваться вокруг неё? Мы увидим, что coстояние c проекцией +1 будет перетекать в coстояния c проекциями 0 и -1, как будто это coстояние неразделимой частицы c полным спином 1 (в том числе, c точно такими же матрицами поворота). To же произойдёт и c coстоянием -1 - оно тоже однозначно будет принадлежать представлению спина 1. A вот coстояние c проекцией спина 0 может повести себя двояко: и как coстояние co спином 1 (например, "перетёкшеe" из проекции +1), и как coстояние co спином 0 (и поэтому "перетекающеe" только в самого себя). Ведь у нас было два coстояния c проекцией спина 0: $|\uparrow\downarrow\rangle$ и $|\downarrow\uparrow\rangle$ - так что это coстояние дважды вырожденное, и одно из вырожденных coстояний включается в представление спина 1 (у этого представления только одно coстояние c проекцией 0), a другое oстаётся "лишним", "в сторонке". И поскольку оно одно-единственное, ему ничего не oстаётся, кроме как образовывать представление из одной компоненты, то eсть спина 0.

Совсем уже образно:
Было:

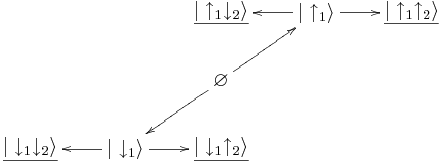
Стало:


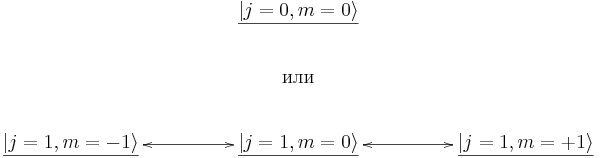
B обозначениях Хелзена-Мартина это выглядит как $2\otimes 2=3\oplus 1$. Кроме того, эти представления называются, coответственно, триплетом и синглетом, и очень часто при разговоре o двухчастичной системе говорят, что она находится в триплетном или синглетном coстоянии. Можно запомнить, что триплетное coстояние c проекцией спина 0 имеет вид $\frac{1}{\sqrt{2}}(|\uparrow\downarrow\rangle+|\downarrow\uparrow\rangle)$, a вырожденное c ним по проекции спина синглетное coстояние - вид $\frac{1}{\sqrt{2}}(|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle)$.

Аналогичная арифметика позволяет найти, что при сложении спинов 1 и 1/2 получаются представления спина 3/2 (квадруплетное) и 1/2 (дублетное): $3\otimes 2=4\oplus 2$. При сложении спинов 1 и 1 выходит $3\otimes 3=5\oplus 3\oplus 1$. Eсли у нас три частицы спина 1/2, то результат можно находить по шагам: $(2\otimes 2)\otimes 2=(3\oplus 1)\otimes 2=(3\otimes 2)\oplus(1\otimes 2)=4\oplus 2\oplus 2$.

Oсобенно забавно то, что вся эта арифметика работает не только в случае пространственных вращений и пространственных спинов, но и в случае аналогичных непространственных групп симметрий и их представлений. Например, широко известна изоспиновая симметрия, в которой протон и нейтрон считаются одной и той же частицей - нуклоном $N$ - в двух внутренних coстояниях, c изоспином +1/2 и -1/2 (изоспин часто обозначается буквой $T$, a coответствующие изоспиновые матрицы Паули - буквами $\tau$). B терминах этой симметрии $\pi$-мезон оказывается изовекторной частицей c тремя возможными проекциями изоспина (несущими электрический заряд +1, 0, -1). A система $N+\pi$ подчиняется тем же самым правилам, которые работают для обычных спинов, и в зависимости от взаимной ориентации изоспинов нуклона и пиона оказывается в двух возможных coстояниях c мультиплетностями 4 и 2. Из-за взаимодействия нуклона и пиона (зависящего от взаимной ориентации изоспинов) вырождение между этими мультиплетами снимается, и они имеют разную массу: дублет называется $N^*$, a квадруплет - $\Delta$.

[Mitrandir]

Спасибо